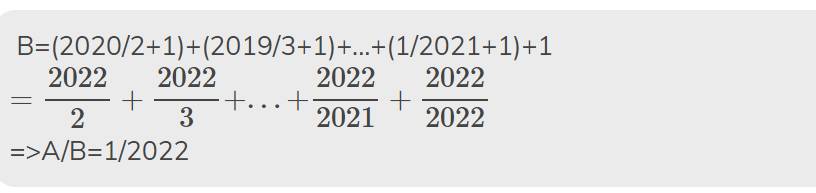A=(-1)×(-1)^2×(-1)^3×(-1)^4×......× (-1)^2020×(-1)^2021
Những câu hỏi liên quan
Câu 24: Cho biểu thức: A=1/2+1/3+1/4+.........+1/2021+1/2022 Và B=2021/1+2020/2+2019/3+.........+3/2019+2020+1/2021
B/A
\(=\dfrac{1+\dfrac{2020}{2}+1+\dfrac{2019}{3}+...+1+\dfrac{1}{2021}+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}\)
\(=\dfrac{2022\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}=2022\)
Đúng 1
Bình luận (0)
1. So sánh
a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\) và B= \(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{13}{60}\)
b) \(C=\dfrac{2019}{2021}+\dfrac{2021}{2022}\) và \(D=\dfrac{2020+2022}{2019+2021}.\dfrac{3}{2}\)
a) Ta có:
2A=2.(12+122+123+...+122020+122021)2�=2.12+122+123+...+122 020+122 021
2A=1+12+122+123+...+122019+1220202�=1+12+122+123+...+122 019+122 020
Suy ra: 2A−A=(1+12+122+123+...+122019+122020)2�−�=1+12+122+123+...+122 019+122 020
−(12+122+123+...+122020+122021)−12+122+123+...+122 020+122 021
Do đó A=1−122021<1�=1−122021<1.
Lại có B=13+14+15+1360=20+15+12+1360=6060=1�=13+14+15+1360=20+15+12+1360=6060=1.
Vậy A < B.
Đúng 2
Bình luận (0)
27 tháng 3 2022 lúc 21:50
Cho A = 1/2+1/3+1/4+...+1/2022 và
B = 2021/1+2020/2+2019/3+...+1/2021.
hứa cho đúng
Bạn kiểm tra đề giúp mình! Bạn yêu cầu gì về giả thiết trên?
Đúng 1
Bình luận (0)
22 tháng 4 2022 lúc 19:58
Tìm a, biết; 1/1×2 + 1/2×3 + 1/3×4 +...+ 1/a × (a + 1) = 2020/2021
=>1-1/2+1/2-1/3+...+1/a-1/(a+1)=2020/2021
=>1-1/(a+1)=2020/2021
=>1/(a+1)=1/2021
=>a+1=2021
=>a=2020
Đúng 0
Bình luận (0)
cho a^1/a^2=a^2/a^3=.......=a^2021/a^2021
cmr:a^1/a^2021=(a^1+a^2+.....+a^2020/a^2+a^3+.....+a^2021)^2020
Ta có \(\frac{a}{a^2}=\frac{a^2}{a^3}=...=\frac{a^{2020}}{a^{2021}}=\frac{a+a^2+....+a^{2020}}{a^2+a^3+...+a^{2021}}\)
=> \(\frac{a}{a^2}=\frac{a+a^2+...+a^{2020}}{a^2+a^3+...+a^{2021}}\)
=> \(\left(\frac{a}{a^2}\right)^{2020}=\left(\frac{a+a^2+...+a^{2020}}{a^2+a^3+...+a^{2021}}\right)^{2020}\)
=> \(\frac{a}{a^2}.\frac{a}{a^2}...\frac{a}{a^2}=\left(\frac{a+a^2+...+a^{2020}}{a^2+a^3+...+a^{2021}}\right)^{2020}\)(2020 thừa số \(\frac{a}{a^2}\))
=> \(\frac{a}{a^2}.\frac{a^2}{a^3}...\frac{a^{2020}}{a^{2021}}=\left(\frac{a+a^2+...+a^{2020}}{a^2+a^3+...+a^{2021}}\right)^{2020}\)(Vì \(\frac{a}{a^2}=\frac{a^2}{a^3}=...=\frac{a^{2020}}{a^{2021}}\))
=> \(\frac{a}{a^{2021}}=\left(\frac{a+a^2+...+a^{2020}}{a^2+a^3+...+a^{2021}}\right)^{2020}\)(đpcm)
22 tháng 9 2021 lúc 0:28
Bài 1: Tính tổng:
a) S = 1+2+3+….+2021 b) P = 1+3+5+……+2021
c) Q = 2+4+6+.......+ 2020 d) M = 1+4+7+.....+298
a) \(S=1+2+3+...+2021\)
\(=\left(2021+1\right).2021:2\)
\(=2043231\)
b) \(P=1+3+5+...+2021\)
\(=\left(2021+1\right).[\left(2021-1\right):2+1]:2\)
\(=2022.1011:2\)
\(=1022121\)
Đúng 1
Bình luận (0)
tính A/B biết:
A=1/2+1/3+1/4+..+1/2021.
B=2020/1+2019/2+...+2/2019+1/2020.
Nhanh giúp mk nhé!
Cần gấp lắm!
số lượng số hạng của dãy số là
( 2021 - 2 ) : 1 + 1 = 2020
tổng của dãy số là
( 2021 + 2) x 2020 : 2 = 2043230
vậy A = \(\frac{1}{2043230}\)
xong a rồi vậy b thì sao bạn
Xem thêm câu trả lời
a,1/2+1/3+1/4+...+1/2020
b,1/2+1/2^2+...+1/2^109
c,1/1*2+1/2*3+...1/2020*2021
Cho \(A=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2022}\)
Và \(B = \dfrac{2021}{1}+\dfrac{2020}{2}+\dfrac{2019}{3}+...+\dfrac{1}{2021}\)
Tính B/A
