
làm được bài nào thì làm giúp mình nha<3
cảm ơn mng nhiều nhắmmm🥺💕💞
Ai có bài nào muốn hỏi thì nhắn tin cho mình nha, mình đag rảnh nên nếu làm được thì mình làm giúp cho nha
toán lớp nào cũng được (lớp 9 trở xuống)
bạn nào muốn thì ghi chữ M và trả lời câu hỏi 1+1=? nha
Trả lời:
1 + 1 = 2
#kin
~~hok tốt~~
mọi người ơi giúp mình bài này với , làm đc bài nào thì giúp mình nha :
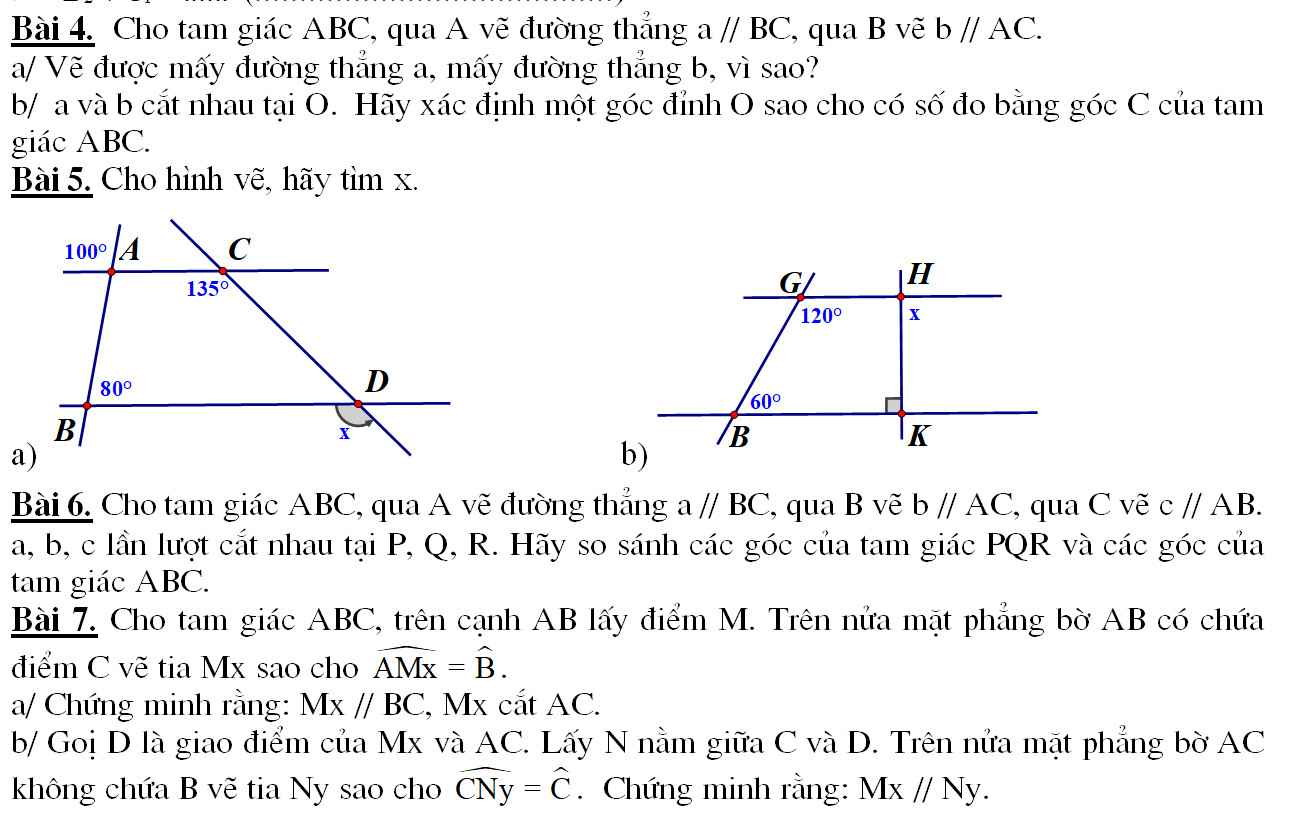
Bài 5:
Ta có : \(\widehat{A_1}+\widehat{A_3}=180^o\) (kề bù)
\(100^o+\widehat{A_3}=180^o\)
\(\widehat{A_3}=80^o\)
Ta có: \(\widehat{A_3}=\widehat{B_1}=80^o\)
\(\widehat{A_3}\) và \(\widehat{B_1}\) ở vị trí đồng vị
\(\Rightarrow AC//BD\)
\(\Rightarrow\widehat{C}_1=\widehat{D_1}=135^o\) (đồng vị)
\(x=135^o\)
b)
Ta có: \(\widehat{G_1}+\widehat{B_1}=180^o\left(120^o+60^o=180^o\right)\)
\(\widehat{G_1}\) và \(\widehat{B_1}\) ở vị trí trong cùng phía
\(\Rightarrow QH//BK\)
\(\Rightarrow\widehat{H_1}=\widehat{K_1}=90^o\)(so le)
\(x=90^o\)
Có bạn nào biết làm câu này không thì giúp mình nha mình đang cần gấp 9 giờ mình phải nộp cho cô rồi nếu được thì mình cảm ơn nhiều chỉ phải làm câu 3 bài 1 thôi nhé
O1=O2( vì 2 góc đối đỉnh)
O3 và O4 thì làm theo cách hai góc kề bù
Vd :O1+O3=180 độ (2 góc kề bù)
Suy ra :120 độ +O3=180 độ
Vậy từ đó tính ra đc O3 ,tương tự O4 cũng vậy
Các bạn vào xem 5 câu hỏi đầu tiên của mình rồi thấy bài nào làm được thì giúp nha(chẳng có ai làm cả TT)
mọi người ơi giúp mình , ai làm đc bài nào thì giúp mình nha :

Vì đg thẳng c vuông góc với đg thẳng b
Đg thăng c vuông góc với đg thẳng a
=》a//b
Giải chi tiết giúp mình! Đừng tắt quá nha. Mn làm đc bài nào thì làm
3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)

Mọi người giúp mình nha .Ai có thể làm bài nào hộ mình thì làm.Ai mà làm được tất thì quá tốt lun. :D
Bạn nào biết làm thì giúp mình 3 bài này nha mình đang cần gấp 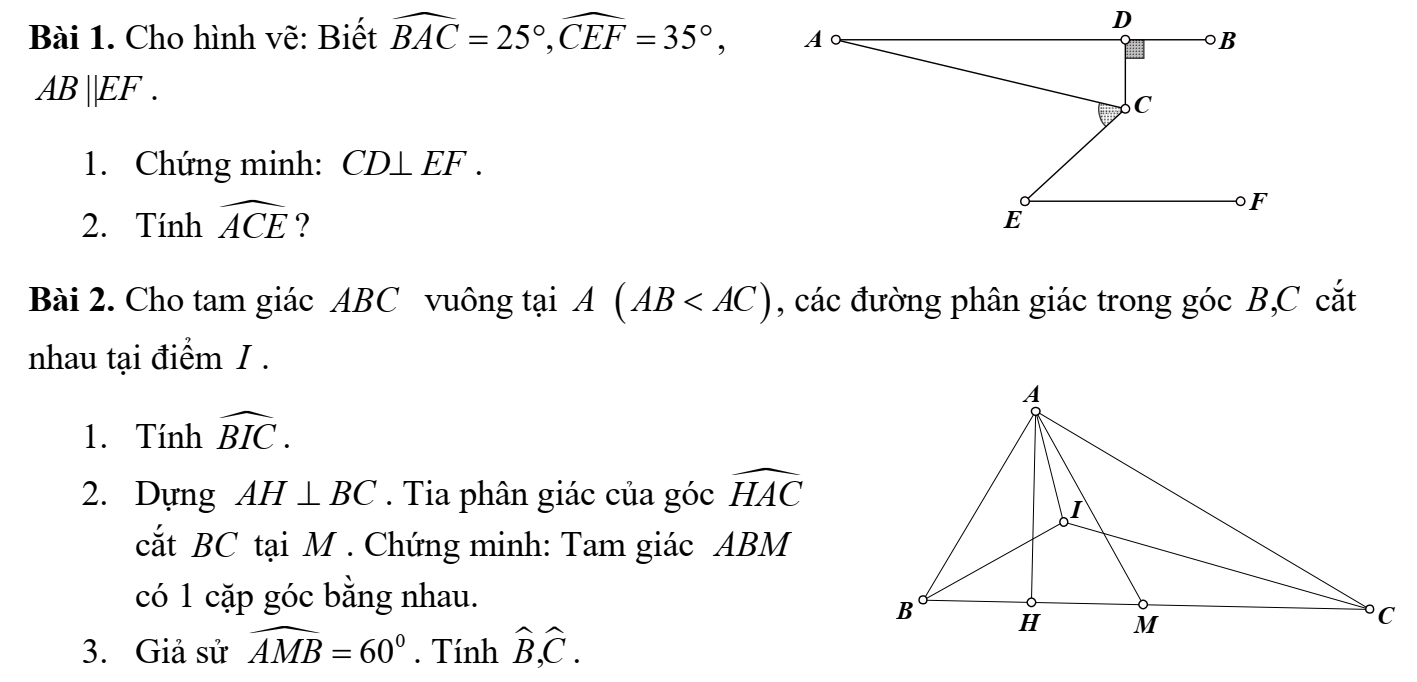
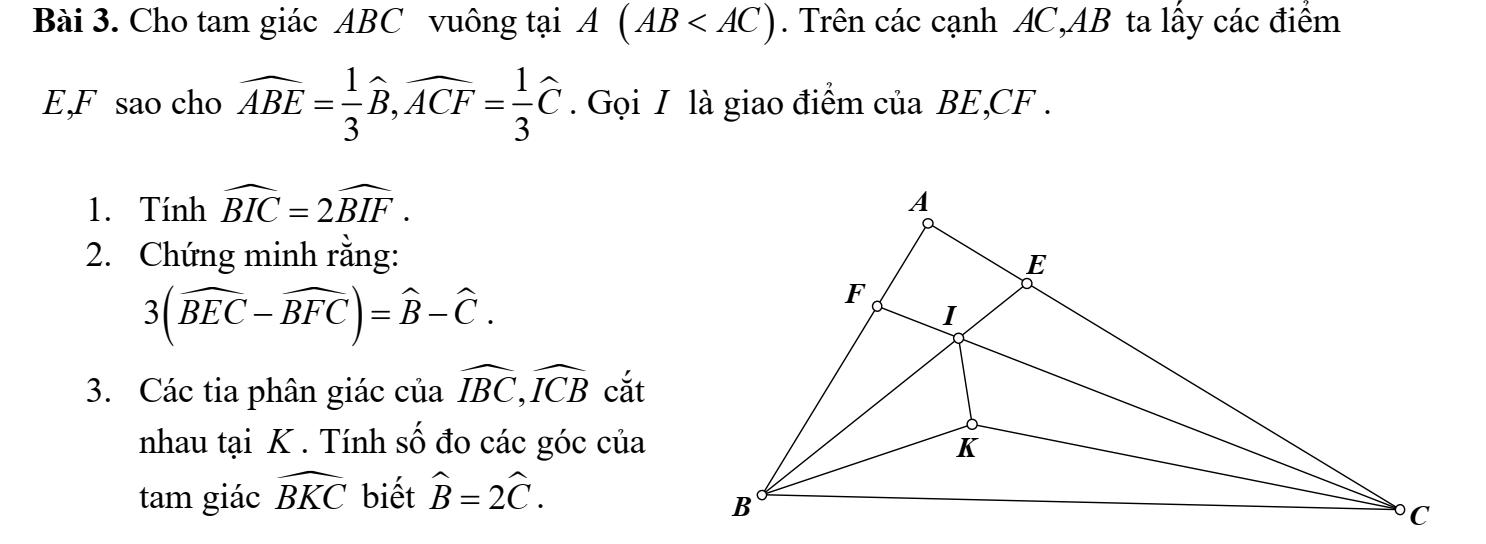
Có bạn nào biết làm 3 bài này không thì giúp mình nha mình đnag cần gấp, 12 giờ mình phải nộp cho thầy rồi thầy này khó tính lắm.Nếu được thì mình cảm ơn nhiều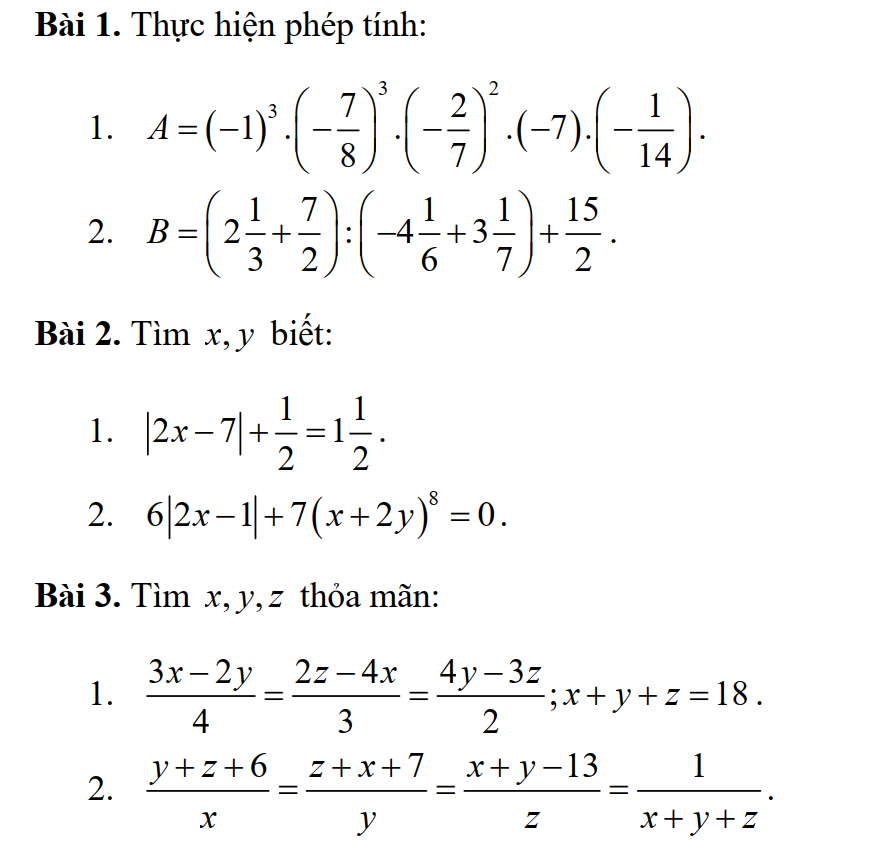
bài 2
1)
/2x-7/+\(\dfrac{1}{2}=1\dfrac{1}{2}\)
/2x-7/+\(\dfrac{1}{2}=\dfrac{3}{2}\)
/2x-7/=1
=> 2x-7=1 hoặc -2x+7 =1
2x=8 hoặc -2x=-6
x=4 hoặc x=3
Bài 1:
1: Ta có: \(A=\left(-1\right)^3\cdot\left(-\dfrac{7}{8}\right)^3\cdot\left(-\dfrac{2}{7}\right)^2\cdot\left(-7\right)\cdot\left(-\dfrac{1}{14}\right)\)
\(=\dfrac{7^3}{8^3}\cdot\dfrac{4}{49}\cdot\dfrac{1}{2}\)
\(=\dfrac{343}{512}\cdot\dfrac{2}{49}\)
\(=\dfrac{7}{256}\)