Cho ba điểm tùy : A;B;C thẳng hàng làm thế nào chỉ đo hai lần mà biết được độ dài của các đoạn thẳng AB;BC và CA

Những câu hỏi liên quan
cho ba điểm A,B,C thẳng hàng và điểm D tùy ý. Tại sao có thể nói
a) nếu ba điểm A,B,D thẳng hàng thì ba điểm B,C,D cũng thẳng hàng
b) nếu ba điểm A,B,D không thẳng hàng thì ba điểm B,C,D cũng không thẳng hàng
GIải
Nếu A , B ,C thẳng hàng và A,B,D thẳng hàng
=> 4 điểm A,B,C,D thẳng hàng
Vậy thì B,C,D cũng thẳng hàng
b) Nếu ba điểm A,B,C thẳng hàng và A,B,D không thẳng hàng
=> D không thẳng hàng với A,B,C
Vậy B,C,D cũng không thẳng hàng
Đúng 0
Bình luận (0)
. Cho hình vuông ABCD, M là một điểm tùy ý trên đường chéo BD. Kẻ ME vuông AB, MF vuông AD .
a) Chứng minh DE=CF .
b) Chứng minh ba đường thẳng DE, BF, CM đồng quy.
Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm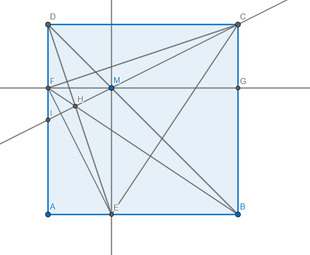
Đúng 1
Bình luận (0)
Cho tam giác $A B C$ và một điểm $M$ tùy ý. Gọi $A^{\prime}, B^{\prime}, C^{\prime}$ lân lượt là các điêm đôi xứng của $M$ qua các trung điểm $K, I, J$ của các cạnh $B C, C A, A B$.
a) Chứng minh ba đường thẳng $A A^{\prime}, B B^{\prime}, C C^{\prime}$ đồng quy tại một điểm $N$.
b) Chứng minh rằng khi $M$ di động thì đường thẳng $M N$ luôn đi qua trọng tâm $G$ của $\triangle A B C$.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:
a) \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;} \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
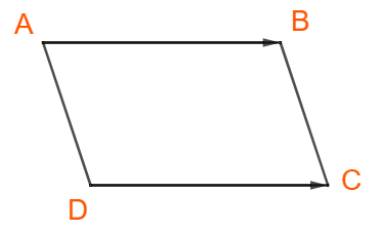
a) ABCD là hình bình hành nên \(\overrightarrow {DC} = \overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0 \)
b) \(\overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)\)
\(= \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) + \left( {\overrightarrow {BA} + \overrightarrow {DC}} \right)\)
\(= \overrightarrow {MB} + \overrightarrow {MD} \) (Vì \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} \))
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho
a
2
+
b
2
+
c
2
3
. Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng A.
1
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là các số thực dương thay đổi tùy ý sao cho a 2 + b 2 + c 2 = 3 . Khoảng cách từ O đến mặt phẳng (ABC) lớn nhất bằng
A. 1 3
B. 3
C. 1 3
D. 1
Đáp án C
Vì OA, OB, OC đôi một vuông góc với nhau 1 d 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
Với d là khoảng cách từ O -> (ABC) suy ra 1 d 2 = 1 a 2 + 1 b 2 + 1 c 2
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức, ta có x 2 a + y 2 b + z 2 c ≥ x + y + z 2 a + b + c
Vậy d m a x = 1 3
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy điểm N sao cho IN MIa) CMR: overrightarrow{BN}-overrightarrow{BA}overrightarrow{MB}b) Tìm các điểm D, C sao cho: overrightarrow{NA}+overrightarrow{NI}overrightarrow{ND} ; overrightarrow{NM}-overrightarrow{BN}overrightarrow{NC}
Đọc tiếp
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy điểm N sao cho IN = MI
a) CMR: \(\overrightarrow{BN}-\overrightarrow{BA}=\overrightarrow{MB}\)
b) Tìm các điểm D, C sao cho: \(\overrightarrow{NA}+\overrightarrow{NI}=\overrightarrow{ND}\) ; \(\overrightarrow{NM}-\overrightarrow{BN}=\overrightarrow{NC}\)
Câu 4 : Cho tam giác ABC cân tại A . Từ A kẻ AH vuông góc với BC tại H , trên đoạn thẳng AH lấy điểm M tùy ý ( M khác A và H ) . Chứng minh rằng :
a) BH=CH
b) BA=BM
Giúp mik vs , đang cần gấp ( kẻ hình luôn nhé )
Bạn xem lại câu b) nha vì BA ko = BM được đâu
Đúng 1
Bình luận (0)
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là trung trựccủaCB
b: SỬa đề; BM=CM
AH là trung trực của BC
=>M nằm trên đường trung trực của BC
=>MB=MC
Đúng 2
Bình luận (0)
Cho tam giác ABC có ba góc nhọn và điểm M tùy ý trong tam giác. Gọi A1, B1, C1 là các điểm đối xứng với M lần lượt qua trung điểm của các cạnh BC, CA, AB. a) Chứng minh AA1, BB1, CC1 đồng quy
b) xác định vị trí của M để hình lục giác AB1CA1BC1 có các cạnh bằng nhau
Vẽ tùy ý ba điểm A, B, C thẳng hàng. Làm thế nào để chỉ đo 2 lần mà biết được độ dài của đoạn thẳng AB, BC, CA.
vi A,B,C thang hang nen B nam giua A va C nen AB+BC=AC
Do do ta chi can biet duoc do dai cua 2 doan la ta co the tim duoc do dai cua ca 3 doan
nho tk mik nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời





















