SÓ. Giúp em giải chi tiết câu 23,34 với ạ🙏🙏😥😥😥. Cần gấp

Những câu hỏi liên quan
Giúp em với ạ. Cần gấp 😥😥😥😥🙏🙏🙏🙏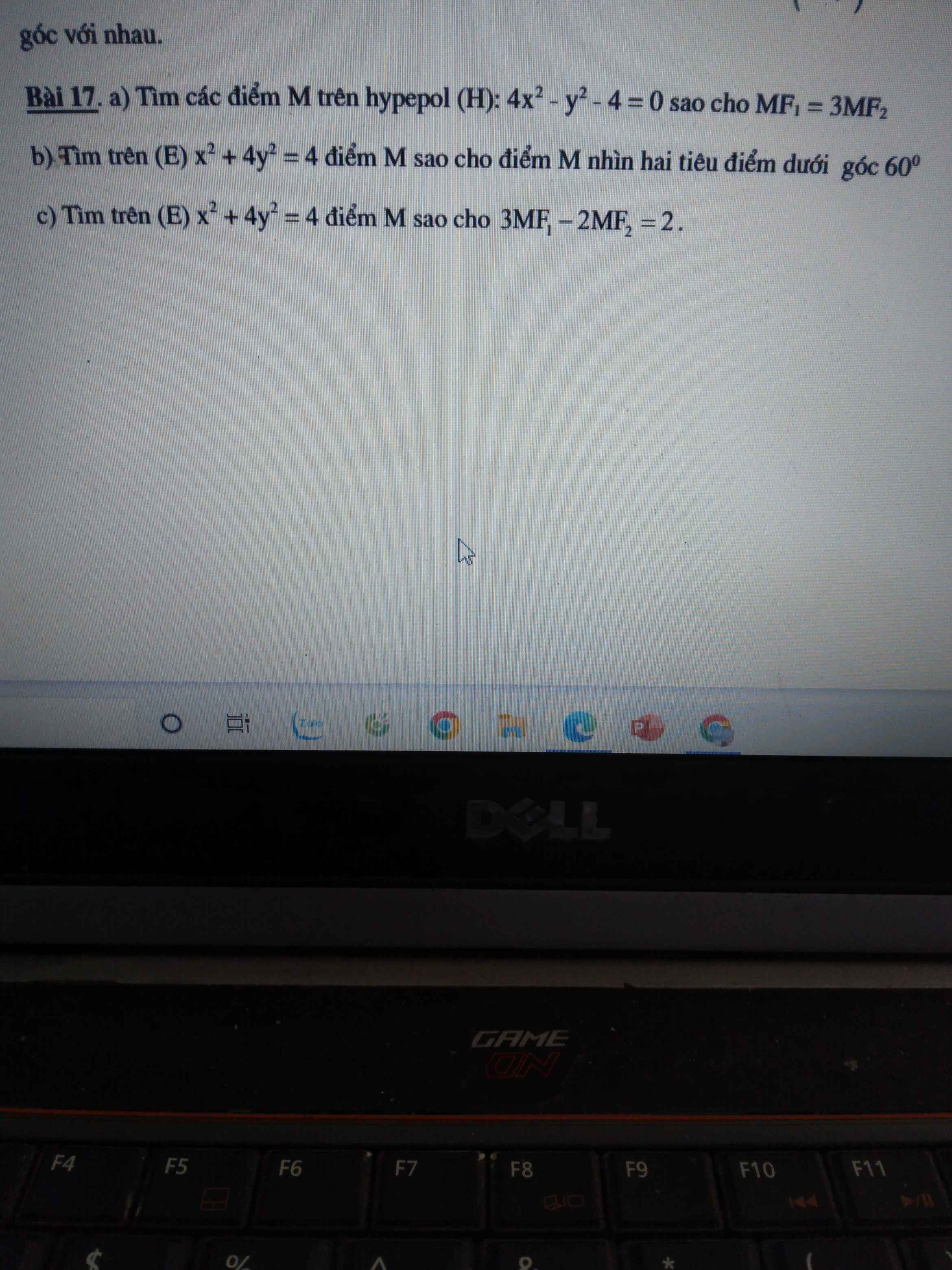
Help!🙏🙏🙏
Cho ab=c^2
Chứng minh rằng : a^2+b^2/a^2+c^2=a/b
Ai đúng nhất nhanh nhất tui tick cho tk.
Gấp nha mai nộp ròi 😥😥😥
a^2+b^2/a^2+c^2=b^2/c^2=b^2/ab=b/a
Bạn ơi , bạn xem lại đề nhé! Mình làm thế này không biết có đúng đề không nữa?
Ta có \(a^2+c^2\ge0\) (gt) mà \(a^2\ge0 \forall a, c^2\ge0 \forall c\)=> \(a\ne0 , c\ne0\)=> \(b\ne0\)( vì \(ab=c^2\))
Với \(a,b,c \ne0\), \(ab=c^2\)=> \(\frac{a}{c}=\frac{c}{b}\)
=> \(\left(\frac{a}{c}\right)^2=\left(\frac{c}{b}\right)^2\)
=> \(\frac{a^2}{c^2}=\frac{c^2}{b^2}=\frac{a^2+c^2}{c^2+b^2}\) mà \(\frac{a}{c}=\frac{c}{b}\)
=> \(\frac{a^2+c^2}{c^2+b^2}=\frac{a}{c}.\frac{c}{b}=\frac{a}{b}\)
Mọi người giúp mình câu ba với ạ, cần gấp lắm ạ!! 😥😥😥
Anh nghĩ với bài kiểm tra em nên tự làm nhé.
Đúng 1
Bình luận (1)
Giúp mình với ạ, mình cần gấp lắm😥😥
a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow1+2sinx.cosx=t^2\Rightarrow2sinx.cosx=t^2-1\)
Phương trình trở thành:
\(3t=2\left(t^2-1\right)\)
\(\Leftrightarrow2t^2-3t-2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2>\sqrt{2}\left(loại\right)\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(1+\dfrac{sinx}{cosx}=2\sqrt{2}sinx\)
\(\Rightarrow sinx+cosx=2\sqrt{2}sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\)
Đúng 0
Bình luận (0)
c.
\(\Leftrightarrow1+sinx+cosx+sinx.cosx=2\)
\(\Leftrightarrow sinx+cosx+sinx.cosx=1\)
Đặt \(sinx+cosx=t\in\left[-\sqrt[]{2};\sqrt{2}\right]\)
\(\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t+\dfrac{t^2-1}{2}=1\)
\(\Leftrightarrow t^2+2t-3=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-3\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Vẽ hai đường thẳng AB và CD vuông góc với nhau tại O.Tia OM là tia phân giác của BOC.Tính AOM
Lời giải chi tiết và vẽ hình đúng mk tik cho 🥰🥰❤️❤️
Mk cần gấp !! Help😍😍😥😥😓😓😥😥☹️
XIN LỖI MK K BT VẼ HÌNH TRÊN NÀY : |_ là vuông góc nhé bạn
Vì AB |_ CD tại O
=>AOD=AOC=DOB=BOC=90 độ
Mà OM là tia pg của góc BOC
=>COM =BOM=45 độ
Ta có góc AOM = AOC +COM
=>GÓC AOM= 90 độ +45 độ=135 độ
mk nhé!
Đúng 0
Bình luận (0)
Chứng minh định lí: “Nếu hai góc có cạnh tương ứng song song thì bằng
nhau nếu hai góc cùng nhọn hoặc cùng tù
mong mn giúp mình đang cần gấp 🙏😥
Giúp mình câu này với ạ, mình đang rất cần ạ😥😥
Giúp em giải chi tiết câu 11 với ạ 🙏🙏
11.
Đường tròn (C) tâm \(I\left(4;3\right)\) bán kính \(R=\sqrt{2}\)
\(d\left(I;\Delta\right)=\dfrac{\left|4+3-11\right|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)
\(\Rightarrow d\left(M;\Delta\right)_{max}=R+d\left(I;\Delta\right)=\sqrt{2}+2\sqrt{2}=3\sqrt{2}\)
Đúng 0
Bình luận (0)
Giúp em với ạ, em đang cần gấp😥
















