Tìm abcd biết
abcd - bcd . 2 = ac
Những câu hỏi liên quan
Tìm số tự nhiên có bốn chữ số abcd biếtabcd+abc+ab+a=4321
Trả lời:
A, Tìm abc biết 90abc : abc = 721
B, Tìm abcd biết abcd - bcd . 2 = ac
C, Tìm abcd biết a + ab + abc = bcd
D, Tìm abc biết abc = ac . 9
E, Tìm ab biết aaaa . 3 + b = baaaa
G, Tìm abcd biết abcd - abc - ab - a = 2086
abcd+bcd*2=ac
abcd - bcd x 2 = ac
abcd - bcd x 2 = ac
a x 1000 + bcd - bcd x 2 = a x 10 + c
a x 1000 - bcd = a x 10 + c
a x 990 - bcd = c
=> a = 1 ; b = 9 ; c = 8 hoặc 9
Nếu c = 9 => bcd = 990 - 9 = 981 (loại)
Vậy c= 8 => bcd = 990 - 8 = 982 => d = 2
Đúng 1
Bình luận (0)
abcd - bcd x 2 = ac
a x 1000 + bcd - bcd x 2 = a x 10 + c
a x 1000 - bcd = a x 10 + c
a x 990 - bcd = c
=> a = 1 ; b = 9 ; c = 8 hoặc 9
Nếu c = 9 => bcd = 990 - 9 = 981 (loại)
Vậy c= 8 => bcd = 990 - 8 = 982 => d = 2
Đúng 1
Bình luận (0)
abcd - bcd x 2 = ac
a x 1000 + bcd - bcd x 2 = a x 10 + c
a x 1000 - bcd = a x 10 + c
a x 990 - bcd = c
=> a = 1 ; b = 9 ; c = 8 hoặc 9
Nếu c = 9 => bcd = 990 - 9 = 981 (loại)
Vậy c= 8 => bcd = 990 - 8 = 982 => d = 2
Đúng 1
Bình luận (0)
Cho tứ diện ABCD có AB ⊥ (BCD) và AB=a√3, BCD là tam giác đều cạnh a.Tính góc giữa: 1) AC và (BCD) 2) AD và (BCD) 3) AD và (ABC)
Cho tứ diện ABCD. Trên AB,AC lấy 2 điểm M,N sao cho MN không song song BC. Gọi O là một điểm nằm trong tam giác BCD. a) Tìm giao tuyến (OMN) và (BCD) b) Tìm giao điểm DB,DC, DA với (OMN) Vẽ hình giúp luôn ạ. Em cảm ơn
a: Trong mp(ABC), gọi E là giao điểm của MN và BC
\(O\in\left(OMN\right);O\in\left(BCD\right)\)
=>\(O\in\left(OMN\right)\cap\left(BCD\right)\)
\(E\in MN\subset\left(OMN\right);E\in BC\subset\left(BCD\right)\)
=>\(E\in\left(OMN\right)\cap\left(BCD\right)\)
Do đó: \(\left(OMN\right)\cap\left(BCD\right)=OE\)
b: Chọn mp(BCD) có chứa DB
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi F là giao của OE với DB
=>F là giao của DB với mp(OMN)
Chọn mp(BCD) có chứa DC
\(\left(OMN\right)\cap\left(BCD\right)=OE\)
Gọi K là giao của OE với DC
=>K là giao của DC với mp(OMN)
Đúng 2
Bình luận (1)
Cho tứ diện ABCD. I và J theo thứ tự là trung điểm của AD và AC, G là trọng tâm tam giác BCD. Xác định giao tuyến của hai mặt phẳng (GID) và (BCD). Tìm thiết diện của mặt phẳng (GIJ) với hình chóp ABCD. Thiết diện là hình gì
1.` Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Tìm điểm M xác định bởi đẳng thức vectơ .overrightarrow{AM}overrightarrow{AB}+overrightarrow{AC}+overrightarrow{AD}.2.Gọi ,MN lần lượt là trung điểm của các cạnh ACvà BDcủa tứdiện .ABCD Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ overrightarrow{IA}+2k-1overrightarrow{IB}+koverrightarrow{IC}+overrightarrow{ID}overrightarrow{0}
Đọc tiếp
1.` Cho tứ diện ABCD. Gọi G là trọng tâm tam giác BCD. Tìm điểm M xác định bởi đẳng thức vectơ .\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\).
2.
Gọi ,MN lần lượt là trung điểm của các cạnh ACvà BDcủa tứdiện .ABCD Gọi I là trung điểm của đoạn MN. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \(\overrightarrow{IA}+2k-1\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
Đúng 1
Bình luận (2)
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD),
A
C
5
a
,
B
C
3
a
,
B
D
4
a
. Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD A.
R
5
a
3
2
B.
R...
Đọc tiếp
Cho tứ diện ABCD có tam giác BCD vuông tại B, AC vuông góc với mặt phẳng (BCD), A C = 5 a , B C = 3 a , B D = 4 a . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABCD
A. R = 5 a 3 2
B. R = 5 a 2 3
C. R = 5 a 3 3
D. R = 5 a 2 2
Đáp án D
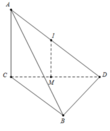
Gọi M là trung điểm của CD đường thẳng qua M song song với AC cắt AD tại trung điểm I của AD. Khi đó I là tâm mặt cầu ngoại tiếp khối tứ diện
Đúng 0
Bình luận (0)