cho tam giác ABC cân tại A. vẽ đường trung tuyến AH và tia phân giác BN sao cho: 2AM=BN. Tính góc A.

Những câu hỏi liên quan
Cho tâm giác ABC cân tại À, vẽ đường trung tuyến AH và tia phân giác BN sao cho :BN=2AH. Tìm góc A
Cho tam giác ABC cân tại A, vẽ trung tuyến AM và phân giác BN sao cho AM=BN/2. Tính góc A
Cho tam giác ABC cân tại A có M là trung điểm của cạnh BC. a) Chứng minh AM vuông góc với BC b) Giả sử góc BAC = 40 độ . Tính góc B và góc C của tam giác ABC. c) Vẽ đường trung tuyến BN của tam giác ABC, trên tia BN lấy điểm D sao cho NB=ND. Chứng minh AB // CD và chứng minh tam giác ACD cân d) Gọi K là giao điểm của AM và BN. Chứng minh BK = 1/3 BD
a) Để chứng minh AM vuông góc với BC, ta sử dụng tính chất của tam giác cân. Vì tam giác ABC cân tại A, nên ta có MA = MC. Vì M là trung điểm của BC, nên ta có MB = MC. Từ đó, ta có MA = MB. Giả sử ta kẻ đường thẳng AM. Vì MA = MB, nên đường thẳng AM là đường trung tuyến của tam giác ABC. Theo tính chất của đường trung tuyến, ta có AM song song và bằng một nửa đoạn thẳng BC. Do đó, AM vuông góc với BC. b) Vì tam giác ABC cân tại A, nên ta có góc BAC = góc BCA. Vì góc BAC = 40 độ, nên góc BCA = 40 độ. Vì tam giác ABC cân tại A, nên tổng hai góc B và góc C là 180 độ - góc BAC = 180 độ - 40 độ = 140 độ. Vì tam giác ABC là tam giác cân, nên góc B = góc C = (180 độ - 140 độ)/2 = 20 độ. Vậy góc B của tam giác ABC là 20 độ và góc C cũng là 20 độ. c) Để chứng minh AB // CD, ta sử dụng tính chất của đường trung tuyến. Vì N là trung điểm của đoạn thẳng BC, nên BN song song và bằng một nửa đoạn thẳng AC. Từ đó, ta có: BN = 1/2 AC. Giả sử ta kẻ đường thẳng CD. Vì NB = ND, nên ta có: 1/2 AC = NB = ND. Do đó, ta có AB // CD. Để chứng minh tam giác ACD cân, ta sử dụng tính chất của đường trung tuyến. Vì D là điểm trên đường trung tuyến BN, nên ta có: ND = 1/2 NB. Từ đó, ta có: ND = 1/2 NB = 1/2 AC. Vì NB = ND và AD là đoạn thẳng chứa đường trung tuyến BN, nên ta có: AD song song và bằng một nửa đoạn thẳng AC. Do đó, tam giác ACD cân. d) Để chứng minh BK = 1/3 BD, ta sử dụng tính chất của điểm giao nhau của hai đường trung tuyến. Vì K là giao điểm của AM và BN, nên ta có: AK = 2/3 AM và BK = 2/3 BN. Vì MA = MB (vì tam giác ABC cân tại A và M là trung điểm của BC), nên AM là đường trung tuyến của tam giác ABC. Từ đó, ta có: AM = 1/2 BC. Vì NB = ND (vì trên tia BN ta lấy điểm D sao cho NB = ND), nên BN cũng là đường trung tuyến của tam giác ABC. Từ đó, ta có: BN = 1/2 AC. Do đó, ta có: AM = 1/2 BC = 1/2 AC. Vì BN = 1/2 AC, nên ta có: BK = 2/3 BN = 2/3 * 1/2 AC = 1/3 AC. Vì AC = BD (vì tam giác ACD cân và D là điểm trên đường trung tuyến BN), nên ta có: BK = 1/3 BD. Vậy ta đã chứng minh BK = 1/3 BD.
Đúng 1
Bình luận (0)
a: ΔABC cân tại A có AM là đường trung tuyến
nên AM vuông góc BC
b: ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
c: Xét tứ giác ABCD có
N là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AB//CD và AB=CD
=>CD=CA
=>ΔCAD cân tại C
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, vẽ trung tuyến AM và đường phân giác BD. Xác định các góc tam giác ABC biết BD = 2AM
từ M vẽ MK// BD ( K thuộc AC )
Tam giác BDC có : M là trung điểm BC; MK//BD
Suy ra : K là trung điểm CD
Do đó: MK là đường trung bình của tam giác BDC.
--> MK = BD/2 = 2AM/2 = AM
---> tam giác AMK cân tại M --> góc MAK = góc MKA
Ta có : góc MAK + góc C = 90 độ
hay góc MKA + góc C = 90 độ
==> góc MKA = 90 độ - góc C (1)
Lại có : góc MKA = góc KMC + góc C = góc DBC + góc C = góc B/2 + góc C = góc C/2 + góc C = 3/2. góc C (2)
Từ (1) (2) ==> 90 độ - góc C = 3/2. góc C
==> 5/2. góc C = 90 độ
==> góc C = 36 độ
==> góc B = 36 độ
==> góc A= 180-36.2=108 độ
Đúng 0
Bình luận (0)
cho tam giác abc cân tại A ,trung tuyến AM và phân giác BN sao cho AM=1/2BN
tính góc BAC
Cho tam giác ABC cân tại A, có AM là đường trung tuyến, BD phân giác góc B, biết BD=2AM, tính các góc trong tam giác ABC
Cho tam giác ABC cân tại A. Tia phân giác của góc BAC cắt BC tại M.
a. Cm tam giác ABM = tam giác ACM
b. Đường trung tuyến BN cắt AM tại G ( N thuộc AC ) Tính BN biết AM = 9cm, BC =8cm.
c. Kẻ đường thẳng qua C và vuông góc với BC cắt tia BN tại E . Cm góc AEB lớn hơn góc ABE.
Giúp mk nha mk cần gấp 😅
Cho tam giác ABC cân tại A. Dựng dường trung tuyến AM và phân giác BD. Tính các góc tam giác ABC, biết BD= 2AM
-Lấy G là trung điểm của CD.
-Ta có: MG là đường trung bình tam giác BDC nên MG=1/2. BD.
-Mà AM=1/2.BD nên MG=AM=> góc MGA=góc MAG=3/2. góc ACB.
-Lại có góc BAC=2.góc MAG=> góc BAC=3.góc ACB và có góc ABC=góc ACB.
=> góc BAC+góc ABC+góc ACB=5.góc ACB=180 độ.
=> góc ABC=góc ACB= 36 độ và góc BAC= 108 độ.
Đúng 0
Bình luận (0)
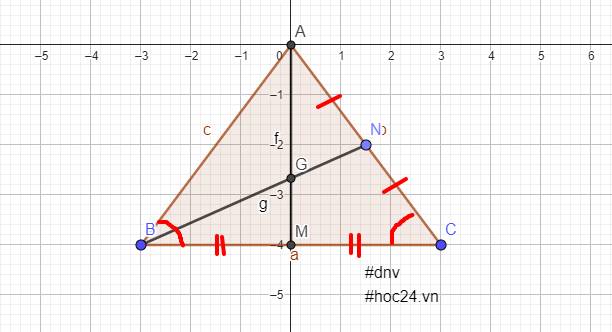
Bài 11. Cho tam giác ABC cân tại A có AM và BN là hai đường trung tuyến cắt nhau tại G.
a) Chứng minh: tam giác AMB = tam giác AMC.
b) Cho biết BN = 15cm . Tính độ dài đoạn thẳng BG
c) Trên tia đối tia MG lấy E sao cho ME = MG . Chứng minh: AG = FG
`@` `\text {dnv}`
`a,`
Xét `\Delta AMB` và `\Delta AMC`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\hat {B} = \hat {C} (\Delta ABC \text {cân tại A})`
`\text {MB = MC (vì AM là đường trung tuyến)`
`=> \Delta AMB = \Delta AMC (c-g-c)`
`b,`
\(\text{Vì AM}\text{ }\cap\text{BN tại G}\)
\(\text{AM, BN đều là đường trung tuyến}\)
`->`\(\text{G là trọng tâm của }\Delta\text{ABC}\)
`@` Theo tính chất của trọng tâm trong tam giác
`->`\(\text{BG = }\dfrac{2}{3}\text{BN}\)
Mà `\text {BN = 15 cm}`
`->`\(\text{BG = }\dfrac{2}{3}\cdot15=\dfrac{15}{3}=5\text{ }\left(\text{cm}\right)\)
Vậy, độ dài của \(\text{BG là 5 cm}\).
`c,` Bạn xem lại đề!
Đúng 2
Bình luận (0)















