`@` `\text {dnv}`
`a,`
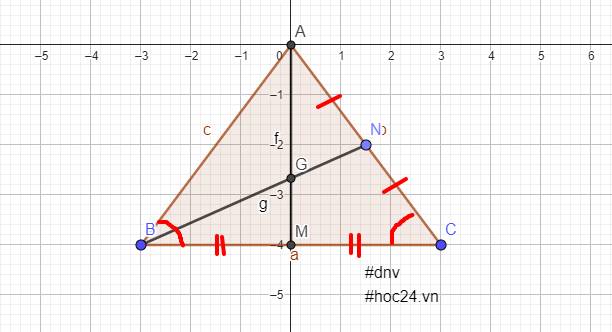
Xét `\Delta AMB` và `\Delta AMC`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\hat {B} = \hat {C} (\Delta ABC \text {cân tại A})`
`\text {MB = MC (vì AM là đường trung tuyến)`
`=> \Delta AMB = \Delta AMC (c-g-c)`
`b,`
\(\text{Vì AM}\text{ }\cap\text{BN tại G}\)
\(\text{AM, BN đều là đường trung tuyến}\)
`->`\(\text{G là trọng tâm của }\Delta\text{ABC}\)
`@` Theo tính chất của trọng tâm trong tam giác
`->`\(\text{BG = }\dfrac{2}{3}\text{BN}\)
Mà `\text {BN = 15 cm}`
`->`\(\text{BG = }\dfrac{2}{3}\cdot15=\dfrac{15}{3}=5\text{ }\left(\text{cm}\right)\)
Vậy, độ dài của \(\text{BG là 5 cm}\).
`c,` Bạn xem lại đề!