x^2-32y-x-3y

Những câu hỏi liên quan
giải hpt:
a) \(\left\{{}\begin{matrix}4x+9y=6\\3x^2+6xy-x+3y=0\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\left(x+y+2\right)\left(2x+2y-1\right)=0\\3x^2-32y^2+5=0\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}2x^2-xy+3y^2=7x+12y-1\\x-y+1=0\end{matrix}\right.\)
Giải các hệ phương trình:
2
x
-
3
2
y
-
5
3
x
+...
Đọc tiếp
Giải các hệ phương trình: 2 x - 3 2 y - 5 = 3 x + 1 3 y - 4 2 x - 3 - 3 y + 2 = - 16
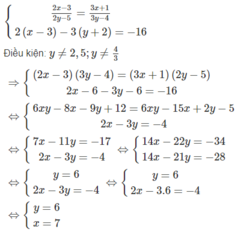
Vậy hệ phương trình đã cho có một nghiệm (x; y) = (7; 6)
Đúng 0
Bình luận (0)
Bài 1: Giải hệ phương trình:left{{}begin{matrix}x^2+32y^29y^4+frac{272}{9}x^2+y^2+xy+43x+4yend{matrix}right.Bài 2: Giải hệ phương trình:left{{}begin{matrix}x^2-xy-3y^2+3x-y-10xy+y^2-x+3y0end{matrix}right.Bài 3: Giải hệ phương trình:left{{}begin{matrix}x^2+3xy-9y^2+23y-170x^2-2xy+3y^2-6y-30end{matrix}right.Ai nhanh và đúng mình sẽ cho đúng và thêm bạn bè nhé. Thanks! Làm ơn giúp mình !!! PLEASE !!!
Đọc tiếp
Bài 1: Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^2+32y^2=9y^4+\frac{272}{9}\\x^2+y^2+xy+4=3x+4y\end{matrix}\right.\)
Bài 2: Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^2-xy-3y^2+3x-y-1=0\\xy+y^2-x+3y=0\end{matrix}\right.\)
Bài 3: Giải hệ phương trình:
\(\left\{{}\begin{matrix}x^2+3xy-9y^2+23y-17=0\\x^2-2xy+3y^2-6y-3=0\end{matrix}\right.\)
Ai nhanh và đúng mình sẽ cho đúng và thêm bạn bè nhé. Thanks! Làm ơn giúp mình !!! PLEASE !!!
Bài 1: Giải hệ phương trình:hept{begin{cases}x^2+32y^29y^4frac{272}{9}x^2+y^2+xy+43x+4yend{cases}}Bài 2: Giải hệ phương trình:hept{begin{cases}x^2-xy-3y^2+3x-y-10xy+y^2-x+3y0end{cases}}Bài 3: Giải hệ phương trình:hept{begin{cases}x^2+3xy-9y^2+23y-170x^2-2xy+3y^2-6y-30end{cases}}Ai nhanh và đúng mình sẽ cho đúng và thêm bạn bè nhé. Thanks! Làm ơn giúp mình !!! PLEASE !!!
Đọc tiếp
Bài 1: Giải hệ phương trình:
\(\hept{\begin{cases}x^2+32y^2=9y^4=\frac{272}{9}\\x^2+y^2+xy+4=3x+4y\end{cases}}\)
Bài 2: Giải hệ phương trình:
\(\hept{\begin{cases}x^2-xy-3y^2+3x-y-1=0\\xy+y^2-x+3y=0\end{cases}}\)
Bài 3: Giải hệ phương trình:
\(\hept{\begin{cases}x^2+3xy-9y^2+23y-17=0\\x^2-2xy+3y^2-6y-3=0\end{cases}}\)
Ai nhanh và đúng mình sẽ cho đúng và thêm bạn bè nhé. Thanks! Làm ơn giúp mình !!! PLEASE !!!
3450 - y = 6440 : 32
y x 1/3 + y x 2/5 = 11/15
3450 - y = 6440 : 32
3450 - y = 201.25
y = 3450- 201.25
y = 3248.75
y x 1/3 + y x 2/5 = 11/15
y x ( 1/3 + 2/5) = 11/15
y x 11/15 = 11/15
y = 11/15 : 11/15
y = 1
Đúng 4
Bình luận (0)
3450 - y = 6440 : 32
3450 - y = 201,25
y =3450 -201,25
y =3248.75
y x 1/3 + y x 2/5 = 11/15
y x( 1/3 + 2/5 ) = 11/15
y x 11/15 = 11/15
y = 11/15 : 11/15
y = 1
Đúng 3
Bình luận (0)
\(3450-y=6440:32\)
\(3450-y=201,25\)
\(y=3450-201,05\)
\(y=3248,75\)
\(y\times\dfrac{1}{3}+y\times\dfrac{2}{5}=\dfrac{11}{15}\)
\(y\times\left(\dfrac{1}{3}+\dfrac{2}{5}\right)=\dfrac{11}{15}\)
\(y\times\dfrac{11}{15}=\dfrac{11}{15}\)
\(y=\dfrac{11}{15}:\dfrac{11}{15}\)
\(y=\dfrac{11}{15}\times\dfrac{15}{11}\)
\(y=1\)
Đúng 2
Bình luận (0)
Giải pt nghiệm nguyên \(xy^2+2xy+x=32y\)
Ta có: \(xy^2+2xy+x=32y \)
⇔ \(x\left(y^2+2y+1\right)=32y\)
⇔\(x=\dfrac{32y}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32y-32+32}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32\left(y+1\right)}{\left(y+1\right)^2}-\dfrac{32}{\left(y+1\right)^2}\)
⇔\(x=\dfrac{32}{y+1}-\dfrac{32}{\left(y+1\right)^2}\)
Để x là số dương ⇒ \(\left(y+1\right)^2\)∈ \(U_{\left(32\right)}\)={-32 ;-16;-8;-4;-2;-1;1;2;4;8;16;32}
Nhưng \(\left(y+1\right)^2\)là số chính phương ⇒ \(\left(y+1\right)^2\)∈ {1;4;16}
⇒\(\left[{}\begin{matrix}\left(y+1\right)^2=1\\\left(y+1\right)^2=4\\\left(y+1\right)^2=16\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y+1=1\\y+1=2\\y+1=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=0\\y=1\\y=3\end{matrix}\right.\)
Thay :
y = 0 ⇒ x = 0
y = 1 ⇒ x = 8
y = 3 ⇒ x = 6
Vậy x;y = ( 0;0) ; ( 8;1) ; ( 6;3)
Đúng 2
Bình luận (0)
Tìm x,y nguyên biết x.(2y-1)2=32y+16
Giải hpt: \(\hept{\begin{cases}2x^2+2y^2+4xy+3x+3y-2=0\\3x^2-32y^2+5=0\end{cases}}\)
Xét phương trình đầu ta có:
2x2 + 2y2 + 4xy + 3x + 3y - 2 = 0
<=> (2x2 + 2xy + 4x) + (2xy + 2y2 + 4y) + (- x - y - 2) = 0
<=> (x + y + 2)(2x + 2y - 1) = 0
Giờ chỉ cần thế ngược lại phương trình thứ 2 là giải ra nhé.
Đúng 0
Bình luận (0)
bài này khó quá mong bạn giải giùm mình,mình suy nghĩ hoài mà ko được.
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn 5x^2 - 32y = 103




















