a) 4x²  - 2x + 3 - 4x.(x - 5) = 7x - 3

--> 4x² - 2x + 3 - 4x² + 20x = 7x - 3

--> 4x² - 2x - 4x² + 20x - 7x = -3 - 3

--> 11x = -6

--> x = \(\frac{-6}{11}\)

b) -3x.(x - 5) + 5.(x - 1) + 3x² = 4x

--> -3x² + 15x + 5x - 5 + 3x² = 4x

--> -3x²  + 15x + 5x + 3x² - 4x = 5 

--> 16x = 5

--> x = \(\frac{5}{16}\)

c) 7x.(x - 2) - 5.(x - 1) = 21x² - 14x² + 3

--> 7x² - 14x - 5x + 5 = 7x² + 3 

--> 7x²  - 14x - 5x - 7x²  = -5 + 3 

--> -19x = -2 

--> x = \(\frac{2}{19}\)

d) 3.(5x - 1) - x.(x - 2) + x² - 13x = 7

--> 15x - 3 - x² + 2x + x² - 13x = 7

--> 15x - x² + 2x + x² - 13x = 3 + 7

--> 4x = 10

--> x = \(\frac{5}{2}\)

e) \(\frac{1}{5}\)x.(10x - 15) - 2x.(x - 5) = 12

--> 2x² - 3x - 2x² + 10x = 12

--> 7x = 12

--> x = \(\frac{12}{7}\)

~ Học tốt ~

a) 4x² - 2x + 3 - 4x(x - 5) = 7x - 3

=> 4x² - 2x + 3 - 4x² + 20x = 7x - 3

=> 18x + 3 = 7x - 3

=> 18x - 7x = -3 - 3

=> 11x = -6

=>  x = -6/11

b) -3x(x - 5) + 5(x - 1) + 3x² = 4x

=> -3x² + 15x + 5x - 5 + 3x² = 4x

=> 20x - 5 = 4x

=> 20x - 4x = 5

=> 16x = 5

=> x = 5/16

\(c,7x\left(x-2\right)-5\left(x-1\right)=21x^2-14x^2+3\)

\(\Leftrightarrow7x^2-14x-5x+5=7x^2+3\)

\(\Leftrightarrow7x^2-7x^2-19x=3-5\)

\(\Leftrightarrow-19x=-2\)

\(\Leftrightarrow x=\frac{2}{19}\)

a) 4x² - 2x + 3 - 4x.(x - 5) = 7x - 3

<=> 18x + 3 = 7x - 3

<=> 18x = 7x - 3 - 3

<=> 18x = 7x - 6

<=> 18x - 7x = -6

<=> 11x = -6

<=> x = -6/11

=> x = -6/11

b) -3x.(x - 5) + 5.(x - 1) + 3x² = 4x

<=> 20x - 5 = 4x

<=> 20x = 4x + 5

<=> 20x - 4x = 5

<=> 16x = 5

<=> x = 5/16

=> x = 5/16

c) 7x.(x - 2) - 5.(x - 1) = 21x² - 14x² + 3

<=> 7x.(x - 2) - 5.(x - 1) = 7x² + 3

<=> 7x² - 19x + 5 = 7x² + 3

<=> 7x² - 19x = 7x² + 3 - 5

<=> 7x² - 19x = 7x² - 2 

<=> 7x² - 19x - 7x² = -2

<=> -19x = -2

<=> x = 2/19

=> x = 2/19

d) 3.(5x - 1) - x.(x - 2) + x² - 13x = 7

<=> 4x - 3 = 7

<=> 4x = 7 + 3

<=> 4x = 10

<=> x = 10/4

=> x = 5/2

e) 1/5x.(10x - 15) - 2x.(x - 5) = 12

<=> x(2x - 3) - 2x(x - 5) = 12

<=> 7x = 12

<=> x = 12/7

=> x = 12/7

1/

a/ \(D=2x\left(10x^2-5x-2\right)-5x\left(4x^2-2x-1\right)\)

\(D=2x\left[10\left(x^2-\frac{1}{2}x-\frac{1}{5}\right)\right]-5x\left[4\left(x^2-\frac{1}{2}x-\frac{1}{4}\right)\right]\)

\(D=20x\left(x^2-\frac{1}{2}x-\frac{1}{5}\right)-20x\left(x^2-\frac{1}{2}x-\frac{1}{4}\right)\)

\(D=20x^3-10x^2-4x-20x^3+10x^2+5x\)

\(D=x\)

b/ Mình xin sửa lại đề:

Tính giá trị biểu thức \(E\left(x\right)=x^5-13x^4+13x^3-13x^2+13x+2012\)

Tại x = 12

\(E\left(x\right)=x^5-\left(x+1\right)x^4+\left(x+1\right)x^3-\left(x+1\right)x^2+\left(x-1\right)x+2012\)

\(E\left(x\right)=x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2-x+2012\)

\(E\left(x\right)=2012-x\)

\(E\left(x\right)=2000\)

2/

a/ \(2x\left(x-5\right)-x\left(3+2x\right)=26\)

<=> \(2x^2-10x-3x-2x^2=26\)

<=> \(-13x=26\)

<=> \(x=-2\)

b/ Bạn vui lòng coi lại đề.

3a/ Ta có \(D=x\left(5x-3\right)-x^2\left(x-1\right)+x\left(x^2-6x\right)-10+3x\)

\(D=5x^2-3x-x^3+x^2+x^3-6x^2-10+3x\)

\(D=-10\)

Vậy giá trị của D không phụ thuộc vào x (đpcm)

Giúp mik vs^^

Thank 

\(a,\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{1}{2}\end{matrix}\right.\\ b,\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\\ c,\Leftrightarrow2x^2-10x-3x-2x^2=26\\ \Leftrightarrow-13x=26\Leftrightarrow x=-2\\ d,\Leftrightarrow x^2-18x+16=0\\ \Leftrightarrow\left(x^2-18x+81\right)-65=0\\ \Leftrightarrow\left(x-9\right)^2-65=0\\ \Leftrightarrow\left(x-9+\sqrt{65}\right)\left(x-9-\sqrt{65}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=9-\sqrt{65}\\9+\sqrt{65}\end{matrix}\right.\)

\(e,\Leftrightarrow x^2-10x-25=0\\ \Leftrightarrow\left(x-5\right)^2-50=0\\ \Leftrightarrow\left(x-5-5\sqrt{2}\right)\left(x-5+5\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=5+5\sqrt{2}\\x=5-5\sqrt{2}\end{matrix}\right.\\ f,\Leftrightarrow5x\left(x-1\right)-\left(x-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(5x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{5}\end{matrix}\right.\\ g,\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ h,\Leftrightarrow x^2+2x+3x+6=0\\ \Leftrightarrow\left(x+3\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\\ i,\Leftrightarrow4x^2-12x+9-4x^2+4=49\\ \Leftrightarrow-12x=36\Leftrightarrow x=-3\)

\(j,\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\Leftrightarrow x=-1\\ k,\Leftrightarrow x^2\left(x-1\right)=4\left(x-1\right)^2\\ \Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a) \(3x\left(x-3\right)-5x\left(x+7\right)\)

\(=3x^2-9x-5x^2-35x\)

\(=-2x^2-44x\)

b) \(\dfrac{1}{5}x\left(10x-15\right)-2x\left(x-5\right)-12\)

\(=2x^2-3x-2x^2+10x-12\)

\(=7x-12\)

a: \(=\dfrac{6x^2+9x+8x+12}{2x+3}=\dfrac{3x\left(2x+3\right)+4\left(2x+3\right)}{2x+3}\)

=3x+4

b: \(=\dfrac{5x^2-2x+15x-6}{5x-2}\)

\(=\dfrac{x\left(5x-2\right)+3\left(5x-2\right)}{5x-2}=x+3\)

c: \(=\dfrac{-8x^2+20x+2x-5-10}{2x-5}=-4x+1+\dfrac{-10}{2x-5}\)

d: \(=\dfrac{14x^2-35x+2x-5}{2x-5}=\dfrac{7x\left(2x-5\right)+\left(2x-5\right)}{2x-5}\)

=7x+1

e: \(=\dfrac{2x^3+x^2+6x^2+3x+12x+6}{2x+1}\)

\(=\dfrac{x^2\left(2x+1\right)+3x\left(2x+1\right)+6\left(2x+1\right)}{2x+1}=x^2+3x+6\)

f: \(=\dfrac{x^3-2x^2+6x^2-12x+x-2}{x-2}=x^2+6x+1\)

g: \(=\dfrac{12x^3+6x^2-4x^2-2x+6x+3}{2x+1}=6x^2-2x+3\)

a: Ta có: \(x\left(2-x\right)+\left(x^2+x\right)=7\)

\(\Leftrightarrow2x-x^2+x^2+x=7\)

\(\Leftrightarrow3x=7\)

hay \(x=\dfrac{7}{3}\)

b: Ta có: \(\left(2x+1\right)^2-x\left(4-5x\right)=17\)

\(\Leftrightarrow4x^2+4x+1-4x+5x^2=17\)

\(\Leftrightarrow9x^2=16\)

\(\Leftrightarrow x^2=\dfrac{16}{9}\)

hay \(x\in\left\{\dfrac{4}{3};-\dfrac{4}{3}\right\}\)

c: Ta có: \(\left(x-4\right)^2-\left(2x+1\right)^2=0\)

\(\Leftrightarrow\left(x-4-2x-1\right)\left(x-4+2x+1\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

d: ta có: \(\dfrac{2x^3-8x^2+10x}{2x}=0\)

\(\Leftrightarrow x^2-4x+5=0\)

\(\Leftrightarrow\left(x-2\right)^2+1=0\)(vô lý)

1

\(-3x\left(x-5\right)+5\left(x-1\right)+3x^2=4-x\)

=> \(-3x^2+15x+5x-5+3x^2=4-x\)

=> \(20x-5=4-x\)

=> \(21x=9\)

=> \(x=\dfrac{3}{7}\)

Vậy x = \(\dfrac{3}{7}\)

2,

\(7x\left(x-2\right)-5\left(x-1\right)=21x^2-14x^2+3\)

=> \(7x^2-14x-5x+5=7x^2+3\)

=> \(-14x-5x+5=3\)

=> \(-19x=-2\)

=> \(x=\dfrac{2}{19}\)

Vậy \(x=\dfrac{2}{19}\)

3,

\(3\left(5x-1\right)-x\left(x-2\right)+x^2-13x=7\)

=> \(15x-3-x^2+2x+x^2-13x=7\)

=> \(4x-3=7\)

=> 4x = 10

=> x = \(\dfrac{5}{2}\)

Vậy x = \(\dfrac{5}{2}\)

4,

\(\dfrac{1}{5}x\left(10x-15\right)-2x\left(x-5\right)=12\)

=> \(2x^2-3x-2x^2+10x=12\)

=> 7x = 12

=> x = \(\dfrac{12}{7}\)

Vậy x = \(\dfrac{12}{7}\)

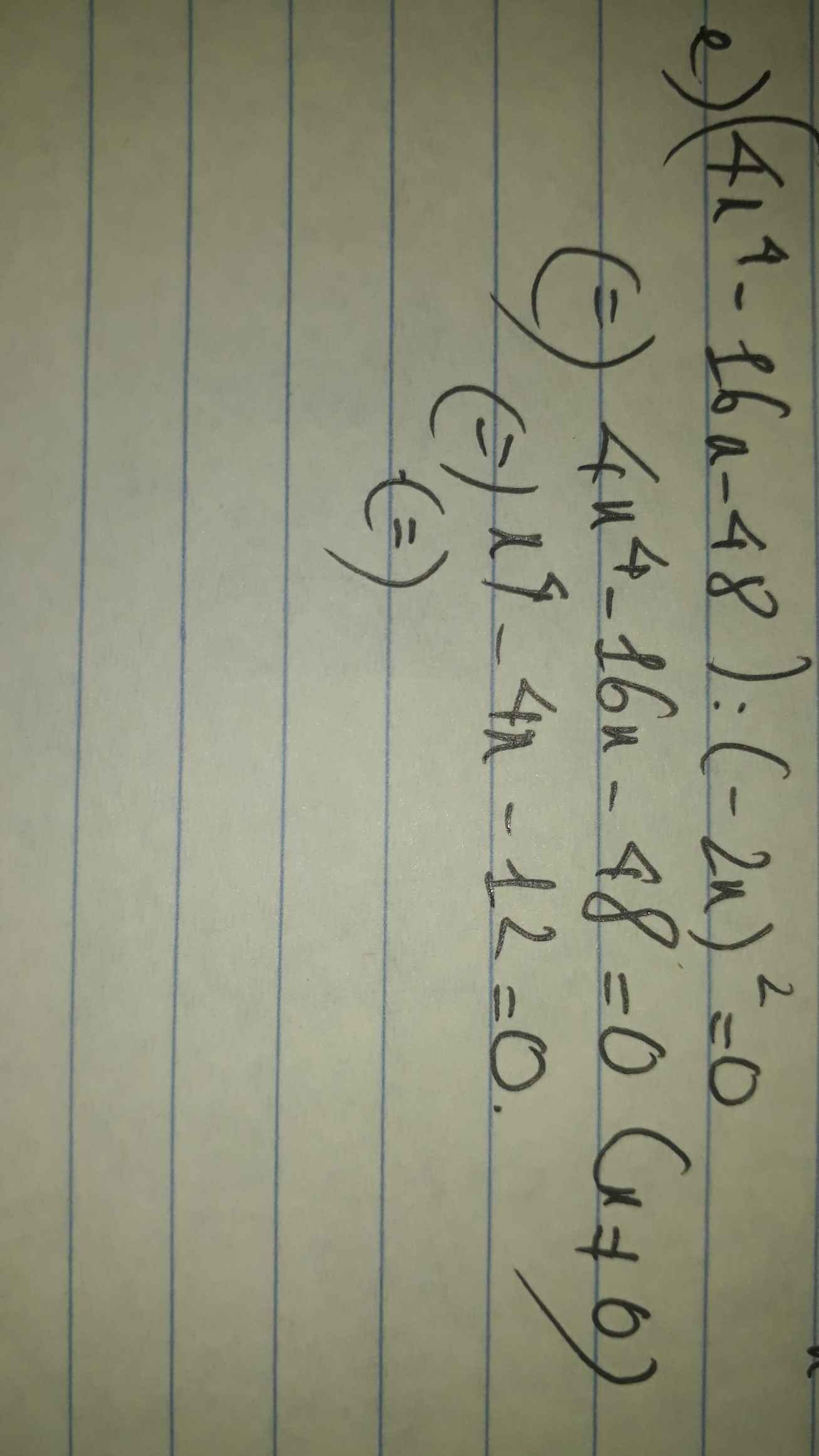
Kkk