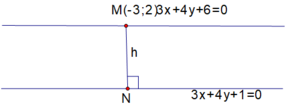
tìm VTPT của đt d biêt d có phương trình -3x^2+4y-5=0

Những câu hỏi liên quan
Cho đt (d): x – 4y + 2 0. Lấy đối xứng của (d) qua Oy ta được đường thẳng có phương trình: A.
−
1
4
x
+
1
2
y
B.
−
1
4
x
−
1
2
y
C.
−
x
+
1
4
y
D.
−
x
+
2...
Đọc tiếp
Cho đt (d): x – 4y + 2 = 0. Lấy đối xứng của (d) qua Oy ta được đường thẳng có phương trình:
A. − 1 4 x + 1 2 = y
B. − 1 4 x − 1 2 = y
C. − x + 1 = 4 y
D. − x + 2 = − 4 y
Đáp án A
Chọn A(2;1) ∈ d => Đ O y : A -> A’( –2; 1)
Chọn B(6;2) ∈ d => Đ O y : B ->B’( –6; 2)
Phương trình đường thẳngđói xứng của (d) qua Oy: − 1 4 x + 1 2 = y
Đúng 0
Bình luận (0)
Cho đt (d): x – 4y + 2 0. Lấy đối xứng của (d) qua Ox ta được đường thẳng có phương trình A.
−
1
4
x
+
1
2
y
B.
−
1
4
x
−
1
2
y
C.
−
x
+
1
4
y
D.
−
x
+
2...
Đọc tiếp
Cho đt (d): x – 4y + 2 = 0. Lấy đối xứng của (d) qua Ox ta được đường thẳng có phương trình
A. − 1 4 x + 1 2 = y
B. − 1 4 x − 1 2 = y
C. − x + 1 = 4 y
D. − x + 2 = − 4 y
Đáp án B
Chọn A(2;1) ∈ d ⇔ Đ O x : A -> A’( 2; –1)
Chọn B(6;2) ∈ d ⇔ Đ O x : B =>B’( 6; –2)
Phương trình đường thẳngđói xứng của (d) qua Oy: − 1 4 x − 1 2 = y
Đúng 0
Bình luận (0)
Cho đường thẳng (d): 3x−4y+5=03x-4y+5=0. Viết phương trình đường thẳng đi qua điểm M(2;1) và song song với đường thẳng d?
A. −3x−4y−2=0-3x-4y-2=0
B. Đáp án khác
C. 3x+4y−2=03x+4y-2=0
D. 3x−4y−2=0
Đường thẳng song song d nên nhận (3;-4) là 1 vtpt
Phương trình:
\(3\left(x-2\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y-2=0\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình
3
x
+
4
y
+
6
0
là ảnh của đường thẳng d có phương trình
3
x
+
4
y
+
1
0
qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
v
→
có độ dài bé nhất. A....
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d' có phương trình 3 x + 4 y + 6 = 0 là ảnh của đường thẳng d có phương trình 3 x + 4 y + 1 = 0 qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ v → có độ dài bé nhất.
A. v → = 3 5 ; − 4 5
B. v → = − 3 5 ; − 4 5
C. v → = ( 3 ; 4 )
Đáp án B
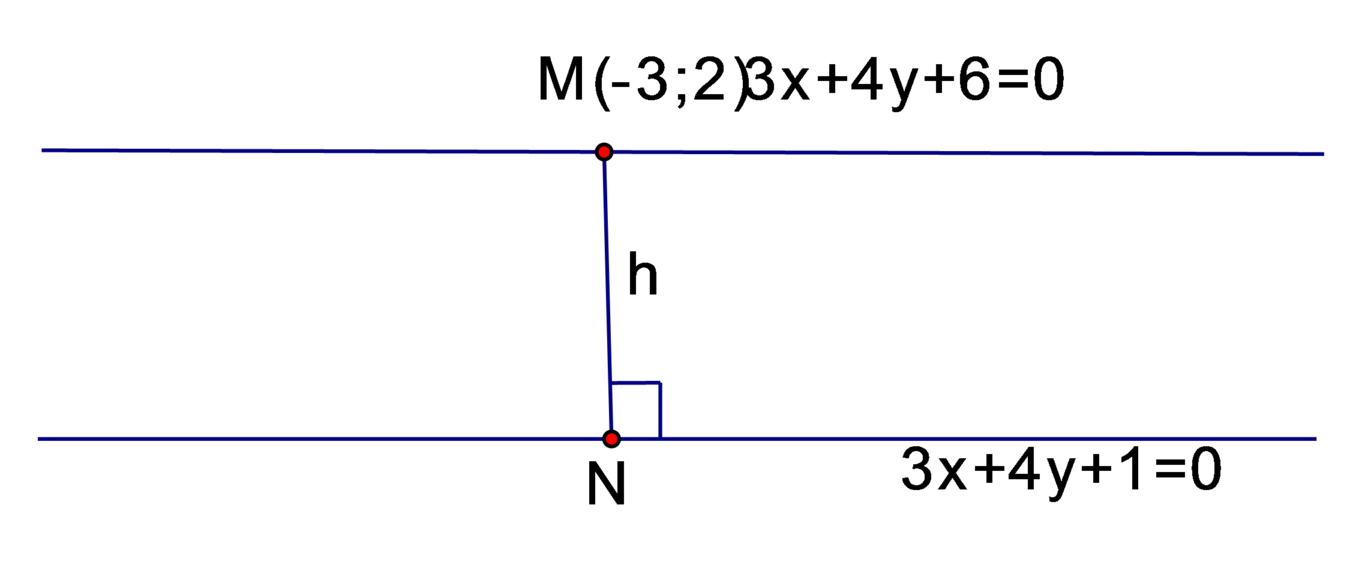
Độ dài véc tơ v → bé nhất đúng bằng khoảng cách h giữa d và d' . h chính là khoảng cách từ M ∈ d tới N ∈ d ' sao cho M N → ⊥ u → 4 ; − 3 trong đó u → là VTCP của cả d và d' .Và khi đó: v → = M N →
Chọn M − 3 ; 2 ∈ d . Ta cần tìm N t ; − 6 − 3 t 4 ∈ d ' sao cho:
M N → t + 3 ; − 14 − 3 t 4 ⊥ u → 4 ; − 3
⇔ 4 t + 12 + 42 + 9 t 4 = 0 ⇔ t = − 18 5
⇒ M N → = − 3 5 ; − 4 5
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình 3x+4y+60 là ảnh của đường thẳng d có phương trình 3x+4y+10 qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
v
→
có độ dài bé nhất. A.
v
→
3
5
;
-...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng d có phương trình 3x+4y+6=0 là ảnh của đường thẳng d có phương trình 3x+4y+1=0 qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ v → có độ dài bé nhất.
A. v → = 3 5 ; - 4 5
B. v → = - 3 5 ; - 4 5
C. v → = 3 ; 4
D. v → = - 3 ; 4
Cho đt (d):3x+2y-4=0.Vt phương trình đt ảnh của đt d qua phép tịnh tiến vecto v(-1;3)
Gọi d' là ảnh của d qua phép tịnh tiến \(\Rightarrow\) d' cùng phương d
Phương trình d' có dạng: \(3x+2y+c=0\)
Lấy \(A\left(0;2\right)\) là 1 điểm thuộc d
\(T_{\overrightarrow{v}}\left(A\right)=A'\Rightarrow A'\in d'\)
\(\left\{{}\begin{matrix}x'=0+\left(-1\right)=-1\\y'=2+3=5\end{matrix}\right.\) \(\Rightarrow A'\left(-1;5\right)\)
Thế vào pt d':
\(3.\left(-1\right)+2.5+c=0\Rightarrow c=-7\)
Phương trình d': \(3x+2y-7=0\)
Đúng 4
Bình luận (0)
Cách 2:
Gọi d' là ảnh của d qua phép tịnh tiến ⇒ d' cùng phương d
Ta có: \(\left\{{}\begin{matrix}x'=x+a\\y'=y+b\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=x'-a=x'-\left(-1\right)=x'+1\\y=y'-b=y'-3\end{matrix}\right.\)
Thay \(x;y\) vào d ta đc:
\(\Rightarrow\left(d'\right):3\left(x'+1\right)+2\left(y'-3\right)-4=0\)
\(\Rightarrow\left(d'\right):3x'+2y'-7=0\)
Vậy ảnh của (d) là \(\left(d'\right):3x+2y-7=0\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 0 và đường tròn (C) có phương trình
x
2
+
y
2
−
2
x
+
4
y
–
4
0
. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
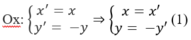
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x+2y-6=0\) và đường tròn (C) có phương trình \(x^2+y^2-2x+4y-4=0\). Tìm ảnh của M, d và (C) qua phép đối xứng qua trục Ox ?
Tìm nghiệm nguyên của phương trình: \(3x^2+4y^2+12x+3y+5=0\)
Giúp mình nhé ai nhank mik tik cho! :D
\(Pt\Leftrightarrow3x^2+12x+4y^2+3y+5=0\)
Coi pt trên là pt bậc 2 ẩn x
Ta có : \(\Delta'=36-12y^2-9y-15\)
\(=-12y^2-9y+21\)
Pt có nghiệm \(\Leftrightarrow\Delta'=-12y^2-9y+21\ge0\)
\(\Leftrightarrow-\frac{7}{4}\le y\le1\)
Mà \(y\inℤ\Rightarrow y\in\left\{-1;0;1\right\}\)
Rồi làm nốt
Đúng 0
Bình luận (0)