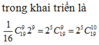Có số tự nhiên n nào thỏa mãn :n2-14n-256 là scp

Những câu hỏi liên quan
Tìm tất cả các số tự nhiên n để \(\sqrt{n^2+14n-256}\)là số tự nhiên
biểu thức đã cho là số tự nhiên khi n^2+14n-256=a^2(a là số tự nhiên)
n^2+14n+49=a^2+49+256=a^2+305
(n+7)^2= a^2+305
vì n là số tự nhiên nên n+7 là số tự nhiên nên (n+7)^2 là số chính phương có dang b^2(b là số tự nhiên)
suy ra a^2+305=b^2
b^2-a^2=305
(b-a)(b+a)=305
vì a và b là số tự nhiên nên a+b là số tự nhiên và b+a>b-a
suy ra b+a là ước tự nhiên của 305={1;5;61;305}
nếu b+a=1 thì b-a=305>b+a(loại)
nếu b+a=5 thì b-a=61>b+a(loại)
nếu b+a=61 thì b-a=5 suy ra a=28 thay vào tìm được n=26
nếu b+a=305 thì b-a=1 suy ra a=152 thay vào tìm đươc n=146
vây n=26 hoặc n=146 tmđb
Đúng 0
Bình luận (0)
Tìm hệ số chứa
x
10
trong khai triển
f
x
1
4
x
2
+
x
+
1
2...
Đọc tiếp
Tìm hệ số chứa x 10 trong khai triển f x = 1 4 x 2 + x + 1 2 x + 2 3 n với n là số tự nhiên thỏa mãn hệ thức A n 3 + C n n - 2 = 14 n
![]()
![]()
![]()
![]()
Tìm hệ số chứa
x
10
trong khai triển
f
x
1
4
x
2
+
x
+
1
2
x
+
2...
Đọc tiếp
Tìm hệ số chứa x 10 trong khai triển f x = 1 4 x 2 + x + 1 2 x + 2 3 n với n là số tự nhiên thỏa mãn hệ thức A n 3 + C n n - 2 = 14 n
A. 2 5 C 19 10
B. 2 5 C 19 10 x 10
C. 2 9 C 19 10
D. 2 9 C 19 10 x 10
tìm tất cả các số tự nhiên n để G=n^2-14n-256 là số chính phương
Đặt \(n^2-14n-256=a^2\)
\(\Leftrightarrow\left(n^2-14n+49\right)-a^2=305\)
\(\Leftrightarrow\left(n-7\right)^2-a^2=305\)
\(\Leftrightarrow\left(n-7+a\right)\left(n-7-a\right)=305=5\cdot61\)
Đến đây làm nốt đi.
Đặt \(G=n^2-14n-256=a^2\)(là số chính phương)
\(\Leftrightarrow n^2-14n+49-305=a^2\)
\(\Leftrightarrow\left(n-7\right)^2-305=a^2\)
\(\Leftrightarrow\left(n-7\right)^2-a^2=305\)
\(\Leftrightarrow\left(n+a-7\right)\left(n-a-7\right)=305=5.61\)
Mà \(n+a-7\ge n-a-7\)nên \(\hept{\begin{cases}n+a-7=61\\n-a-7=5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}n+a=68\\n-a=12\end{cases}}\Leftrightarrow n=\frac{68+12}{2}=40\)
Vậy n = 40 thì \(G=n^2-14n-256\)là số chính phương
Thiếu trường hợp:
305 = 5. 61 = 305 . 1
n là số tự nhiên nhưng a có thể là số âm em nhé! Vì thế không thể kết luận \(n+a-7\ge n-a-7.\)
Với n là số tự nhiên thỏa mãn 2^n=256. khi đó n=...
2^n=256
=>n=8
ok
muốn giải chi tiết thì tích mình đã
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
với n là số tự nhiên thỏa mãn thì 2n = 256
tìm n :
Ta thấy 2.2.2.2 thì dược 1 số có tận cùng là 6
Vậy cứ 4 số 2 nhân lại thì dược một số có tận cùng là 6
Vì 24 = 16
mà 16 .16 = 256 nên 28 = 256
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. a) Tìm n∈N để: \(\left(23-n\right)\left(23+n\right)\) là SCP.
b) Tìm 3 số lẻ liên tiếp mà tổng bình phương của chúng là 1 SCP.
2. a) Tìm nghiệm nguyên: \(x^{11}+y^{11}=11z\)
b) Tìm số tự nhiên n thỏa mãn: \(361\left(n^3+5n+1\right)=85\left(n^4+6n^2+n+5\right)\)
Tìm hệ số chứa x^10 trong khai triển f(x)=(1/4x^2+x+1)(x+2)^3n với n là số tự nhiên thỏa mãn hệ thức A^3n+C^n-2n=14n
Xem chi tiết
 Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Xài cái này gõ bài đi bạn, thề như này hiểu chết liền á :(
Đúng 0
Bình luận (0)
giúp mình câu này với:
tìm các số tự nhiên n thỏa mãn:
a> n^2 + 6n + 3 là SCP
giả sử \(n^2+6n+3\) là SCP
Đặt \(n^2+6n+3=k^2\)
\(\Rightarrow\left(n^2+6n+9\right)-k^2-6=0\\ \Rightarrow\left(n+3\right)^2-k^2=6\\ \Rightarrow\left(n-k+3\right)\left(n+k+3\right)=6\)
Vì \(n\in N\Rightarrow\left\{{}\begin{matrix}n-k+3\in Z,n+k+3\in Z\\n-k+3< n+k+3\\n-k+3,n+k+3\inƯ\left(6\right)\end{matrix}\right.\)
rồi bạn lập bảng ra, tự lm tiếp nhé
Đúng 0
Bình luận (0)