mình cần giải bài 4 và 5 thôi nhé

Bài 3: 

a: =>-10<x<3

b: \(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\8-y=0\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(3;8\right)\)

Bài 4: 

\(\Leftrightarrow6n+4-15⋮3n+2\)

\(\Leftrightarrow3n+2\in\left\{-1;5\right\}\)

hay \(n\in\left\{-1;1\right\}\)

Bài 3: 

-1<x<7

Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
      => 4   =   1   + DC
      => DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có: 
   \(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
   \(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm

Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có: 
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

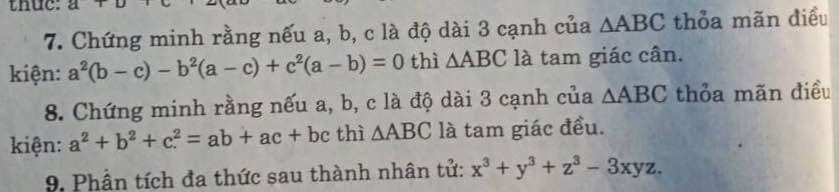
Bài 9:

x³+y³+z³-3xyz=(x+y+z)(x²+y²+z²-xy-yz-zx)

Bài 9:

ta óc hằng đẳng thức x³+y³+z³=(x+y+z)(x²+y²+z²-xy-yz-zx)+3xyz

⇒x³+y³+z³-3xyz=(x+y+z)(x²+y²+z²-xy-yz-zx)+3xyz-3xyz

                       = (x+y+z)(x²+y²+z²-xy-yz-zx)+3xyz

Bài 9:

Ta có: \(x^3+y^3+z^3-3xyz\)

\(=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz\)

\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)

\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)

Bài 3: 

a: =>-10<x<3

b: \(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\8-y=0\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(3;8\right)\)

Bài 4: 

\(\Leftrightarrow3n+2\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)

hay \(n\in\left\{-1;1\right\}\)

Đặt \(m=a^2,n=b^2\)

Ta đưa bài toán về dạng tìm GTLN và GTNN của \(A=m-3mn+2n\)

Khi đó ta suy ra từ giả thiết :

\(\left(m+n+1\right)^2+3mn+1=4m+5n\)

\(\Rightarrow m-3mn+2n=\left(m+n+1\right)^2+1-3m-3n\)

\(=\left(m^2+n^2+2mn+2m+2n+1\right)+1-3n-3m\)

\(=m^2+n^2+2mn-m-n+2\)

\(=m^2+m\left(2n-1\right)+n^2-n+2\)

\(=m^2+m\left(2n-1\right)+\frac{\left(2n-1\right)^2}{4}+\frac{7}{4}\)

\(=\left(m+\frac{2n-1}{2}\right)^2+\frac{7}{4}\ge\frac{7}{4}\)

Hay \(A\ge\frac{7}{4}\) . Đẳng thức xảy ra khi \(m=\frac{1-2n}{2}\)

Tới đây bạn tự suy ra nhé ^^