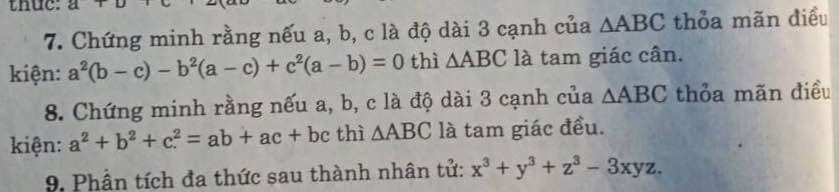Bài 9:
x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)
Bài 9:
ta óc hằng đẳng thức x3+y3+z3=(x+y+z)(x2+y2+z2-xy-yz-zx)+3xyz
⇒x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx)+3xyz-3xyz
= (x+y+z)(x2+y2+z2-xy-yz-zx)+3xyz
Bài 9:
Ta có: \(x^3+y^3+z^3-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)
Bài 8:
Ta có: \(a^2+b^2+c^2=ab+ac+bc\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
\(\Leftrightarrow a=b=c\)