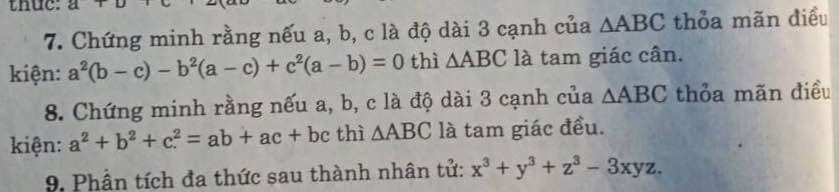16)
a) Tam giác ABC vuông tại A : \(AB^2+AC^2=BC^2\)
BC=10 ⇒FC=10-5.2=4.8
b) Tam giác ABC và tam giác FEC có
C chung
\(\dfrac{AC}{FC}=\dfrac{BC}{EC}=0.6\)
Do đó tam giác ABC đồng dạng với tam giác FEC (C-G-C)
c)⇒Góc FEC=ABC=AEM
Tam giác MAE và tam giác MFB có
Góc M chung
Góc AEM = MBF (CMT)
⇒ 2 Tam giác đồng dạng (G-G)
⇒\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)⇒ MA.MB=MF.MB
a) Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) (Định lí Py-ta-go)
=> \(BC^2=6^2+8^2=100\)
=> BC = 10 (cm)
=> CF = BC\(-\)BF = 10 - 5,2 = 4,8 (cm)
Vậy BC = 10 cm ; CF = 4,8 cm
b) Xét \(\Delta CAB\) và \(\Delta CFE\) có
\(\left\{{}\begin{matrix}\widehat{C}:chung\\\dfrac{CF}{CE}=\dfrac{CA}{CB}\left(\dfrac{4,8}{6}=\dfrac{8}{10}=\dfrac{4}{5}\right)\end{matrix}\right.\)
=>\(\Delta CAB\sim\Delta CFE\) (c-g-c)
Vậy \(\Delta CAB\sim\Delta CFE\)
c) Xét \(\Delta MAEvà\Delta MFB\) có
\(\left\{{}\begin{matrix}\widehat{M}:chung\\\widehat{MAE}=\widehat{MFB}=90^0\end{matrix}\right.\)
=> \(\Delta MAE\sim\Delta MFB\) (g-g)
=> \(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=> MA.MB = MF.ME
Vậy MA.MB = ME.MF
d) Xét \(\Delta BMF\) và \(\Delta BCA\) có
\(\left\{{}\begin{matrix}\widehat{B}:chung\\\widehat{BFM}=\widehat{BAC}=90^0\end{matrix}\right.\)
=> \(\Delta BMF\) \(\sim\)\(\Delta BCA\) (g-g)
=> \(\dfrac{MF}{AC}=\dfrac{BF}{BA}\)
=> MF = \(\dfrac{8.5,2}{6}\) = \(\dfrac{104}{15}\approx6,9\left(cm\right)\)
Vậy MF \(\approx6,9\left(cm\right)\)
Bài 18:
*Tính BC
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+28^2=1225\)
hay BC=35(cm)
Vậy: BC=35cm
Bài 18:
*Tính DC
Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{BD}{21}=\dfrac{CD}{28}\)
mà BD+CD=BC=35cm(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)
Do đó:
\(\dfrac{CD}{28}=\dfrac{5}{7}\)
hay CD=20(cm)
Vậy: CD=20cm
Bài 18:
*Tính ED
Xét ΔABC có
D\(\in\)BC(Gt)
E\(\in\)AC(Gt)
DE//AB(Gt)
Do đó: \(\dfrac{ED}{AB}=\dfrac{CD}{BC}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow\dfrac{ED}{21}=\dfrac{20}{35}\)
hay ED=12(cm)
Vậy: ED=12cm















 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !



 Giup mình vs mình đg cần gấp cảm ơn mn trước ạ
Giup mình vs mình đg cần gấp cảm ơn mn trước ạ