Giúp vs ạ mik rất gấp

Những câu hỏi liên quan
Giúp mik vs ạ!!! Thật sự rất gấp ạ!!! Rất mong nhận đc câu tl của các bạn!!!
Xét tam giác ABC có: góc A+góc B+góc C=180o
=>Góc B+góc C=180o-góc A=180o-60o=120o
Tổng tia phân giác của góc B và góc C là (góc B)/2+(góc C)/2
=(góc B+góc C)/2=120o/2=60o=>góc IBC+góc ICB=60o
Xét tam giác BIC có: góc IBC+góc ICB+góc BIC=180o
=>Góc BIC=180o-(góc IBC+góc ICB)=180o-60o=120o
Vậy góc BIC=60o
Đúng 1
Bình luận (0)
Giúp mik vs!!!! mik cần gấp lắm ạ!!!!!!!
Giải chi tiết và chính xác giúp mình vs!!!!CẢM ƠN RẤT NHIỀU ẠAAAA
!!!!!!!!!!!!!!!!!!!!!!!!!!

Bài 4:
a: a\(\perp\)c
b\(\perp\)c
Do đó: a//b
Đúng 1
Bình luận (0)
ai cs thể giải giúp mik VD3 vs đc k ạ mình đg cần rất rất gấp
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)
Đúng 2
Bình luận (2)
GIÚP MIK LM BÀI NÀY VS Ạ . MIK ĐANG CẦN RẤT LÀ GẤP MONG BN THÔNG CẢM ! THANK YOU!


1B
2 bạn có chép đúng đề?
3D
4B
5A
6A
7A
8A
9B
10B
11C
12A
13C
14B
15A
16C
Đúng 1
Bình luận (0)
Mn ơi giúp mik vs. Mik thực sự cần rất gấp ạ.Mong mn có thể trả lời giúp mik trước sáng mai hoặc trước tối mai ạ.Cảm ơn mn ạ
Bài 5:
\(A=2A-A=2^2+2^3+...+2^{107}-2-2^2-...-2^{2016}=2^{107}-2\)
\(2\left(A+2\right)=2^{2x}\\ \Rightarrow2\left(2^{107}-2+2\right)=2^{2x}\\ \Rightarrow2^{108}=2^{2x}\\ \Rightarrow2x=108\\ \Rightarrow x=54\)
Đúng 1
Bình luận (0)
Bài 3:
Gọi số học sinh lớp 7A, 7B lần lượt là a,b
Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{8}=\dfrac{y}{9}\\y-x=5\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-1}=\dfrac{5}{1}=5\)
\(\dfrac{x}{8}=5\Rightarrow x=40\\ \dfrac{y}{9}=5\Rightarrow y=45\)
Vậy số học sinh lớp 7A, 7B lần lượt là 40, 45 học sinh
Đúng 1
Bình luận (1)
Giúp mik trl nốt bài 1 và bài 4 vs ạ
Đúng 0
Bình luận (0)
Mô tả thí nghiệm quan sát đường phổ?
Mn ơi giúp mik vs, mik đang cần rất gấp ạ, thanks mn trc nhé!
Em hãy thuyết minh về đại hội thể dục thể thao ở địa phương em.
Mng giúp mik vs ạ, mik đag cần rất gấp.
Cảm ơn mng nhìu <3
Giúp mik giải bài tập toán vs ạ mik cảm ơn rất nhiều ạ 
Bài cuối mình không thấy rõ đề nhưng mình đoán là thế này bạn nhé.
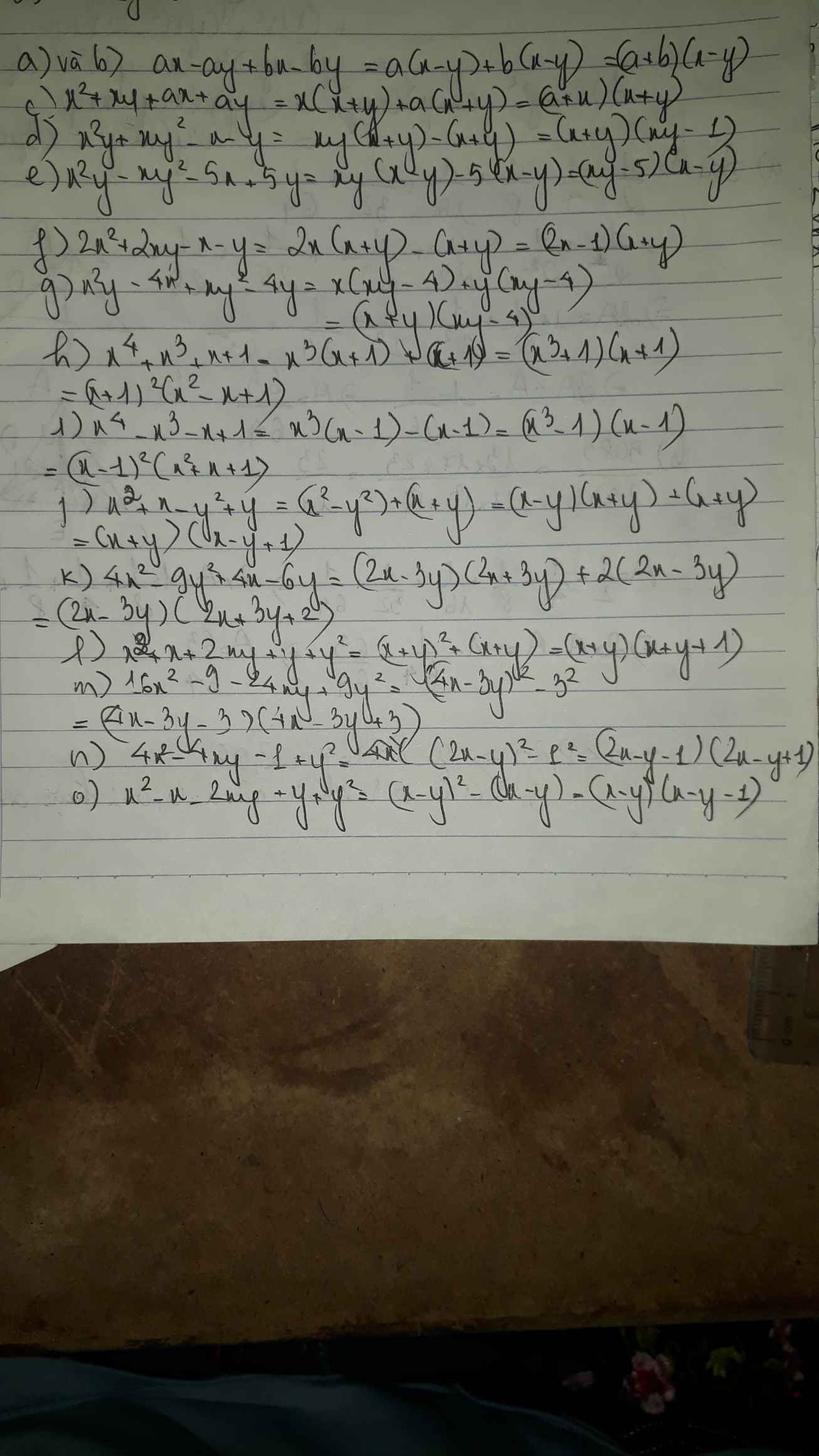
Đúng 1
Bình luận (1)
a.
$ax-ay+bx-by=(ax-ay)+(bx-by)=a(x-y)+b(x-y)$
$=(a+b)(x-y)$
b. Trùng phần a
c.
$x^2+xy+ax+ay=(x^2+xy)+(ax+ay)=x(x+y)+a(x+y)$
$=(x+a)(x+y)$
d.
$x^2y+xy^2-x-y=(x^2y+xy^2)-(x+y)$
$=xy(x+y)-(x+y)=(xy-1)(x+y)$
Đúng 1
Bình luận (1)
e.
$x^2y-xy^2-5x+5y=(x^2y-xy^2)-(5x-5y)$
$=xy(x-y)-5(x-y)=(x-y)(xy-5)$
f. Biểu thức không phân tích được thành nhân tử
g.
$x^2y-4x+xy^2-4y$
$=(x^2y+xy^2)-(4x+4y)=xy(x+y)-4(x+y)=(x+y)(xy-4)$
h.
$x^4+x^3+x+1=(x^4+x^3)+(x+1)$
$=x^3(x+1)+(x+1)=(x^3+1)(x+1)=(x+1)(x^2-x+1)(x+1)$
$=(x+1)^2(x^2-x+1)$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mik vs mik cần rất gấp!





















