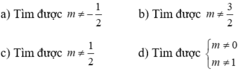Các bạn ơi phương trình bậc to ntn thì giải làm sao ạ :> 4m^3 - 10m^2 +7m -1 =0

Những câu hỏi liên quan
Các bạn giúp mik giải chi tiết phương trình trên làm ntn để ra x=15 với (phần màu đỏ mik đánh dấu ý ạ)
\(\dfrac{x}{12}+\dfrac{1}{4}=\dfrac{x}{10}\)
\(\leftrightarrow\)\(\dfrac{5x}{60}+\dfrac{15}{60}=\dfrac{6x}{60}\)
\(\leftrightarrow\)\(5x+15=6x\)
\(\leftrightarrow\)\(15=6x-5x\)
\(\leftrightarrow\)\(15=x\)
Đúng 1
Bình luận (0)
Cho phương trình bậc hai x²-2x-m²=0 (*) m là tham số a) Giải phương trình (*) ứng với m=1 b) Với m nào thì phương trình (*) có 2 nghiệm phân biệt Giải giúp em với ạ
a: Khi m=1 thì phương trình sẽ là x^2-2x-1=0
=>x^2-2x+1-2=0
=>(x-1)^2=2
=>\(x=\pm\sqrt{2}+1\)
b: Δ=(-2)^2-4*1*(-m^2)=4m^2+4>=4>0
=>Phương trình luôn có hai nghiệm phân biệt
Đúng 2
Bình luận (0)
Các bạn ơi ! Giúp mik với.....B1: Xác định m để phương trình sau có hai nghiệm , nghiệm này bằng hai lần nghiệm kia: ^{x^2-2left(m-2right)x-4m0}B2: Tìm m để phương trình sau có nghiệm âm: frac{1-x}{m-1}-frac{x+1}{1+m}frac{2x+5}{1-m^2}left(mnepm1right)B3: Giải và biện luận phương trình: frac{ax-1}{4}-frac{2left(x-aright)}{3}frac{a+4}{6}B4: Cho a,b,c là ba cạnh của một tam giác chứng minh rằng : 1 frac{a}{b+c}+frac{b}{c+a}+frac{c}{a+b} 2B5: Cho phương trình : left(m^2-4right)x+2mleft(1right) ...
Đọc tiếp
Các bạn ơi ! Giúp mik với.....
B1: Xác định m để phương trình sau có hai nghiệm , nghiệm này bằng hai lần nghiệm kia: \(^{x^2-2\left(m-2\right)x-4m=0}\)
B2: Tìm m để phương trình sau có nghiệm âm: \(\frac{1-x}{m-1}-\frac{x+1}{1+m}=\frac{2x+5}{1-m^2}\left(m\ne\pm1\right)\)
B3: Giải và biện luận phương trình: \(\frac{ax-1}{4}-\frac{2\left(x-a\right)}{3}=\frac{a+4}{6}\)
B4: Cho a,b,c là ba cạnh của một tam giác chứng minh rằng : \(1< \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< 2\)
B5: Cho phương trình : \(\left(m^2-4\right)x+2=m\left(1\right)\)
Với điều kiện nào của m thì phương trình (1) là một phương trình bậc nhất . Tìm nghiệm của phương trình trên với tham số là m.
Ai làm đúng thì mình tích cho nhé !!! Mik cân gấp các bạn nào có cách giải nào thì trả lời nhé !!!! Nghỉ Tết mà nhiều bài quá :)) :v
Giải phương trình bậc hai sau:
x mũ 2 +x-2=0
mình giải lại bài lớp 9 thử nhá,chớ bạn nào làm đk thì cứ giải giúp mk nhé
x^2 + x - 2 = 0
<=> ( x^2 - x ) + ( 2x - 2 ) = 0
<=> x . ( x - 1 ) + 2 . ( x - 1 ) = 0
<=> ( x - 1 ) . ( x + 2 ) = 0
<=> x - 1 = 0 hoặc x + 2 = 0
<=> x = 1 hoặc x = -2
Vậy .......
Tk mk nha
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để các phương trình sau là phương trình bậc nhất:a)
4
m
2
+
4
m
+
1
x
+
5
0
;b)
m
−
3
2
x
−...
Đọc tiếp
Tìm các giá trị của tham số m để các phương trình sau là phương trình bậc nhất:
a) 4 m 2 + 4 m + 1 x + 5 = 0 ;
b) m − 3 2 x − 7 = 0 ;
c) m 2 4 − m 4 + 1 16 x − 2 m + 1 = 0 ;
d) mx + 1 − 2 m + 2 = 0 .
a)Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn ? x – 20; ; ;2x2 + 3 0 ; 4– 0,2x 0 b)Hãy giải các phương trình bậc nhất một ẩn có ở câu a) ?
Đọc tiếp
a)Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn ?
x – 2=0; ![]() ;
; ![]() ;2x2 + 3 = 0 ; 4– 0,2x = 0
;2x2 + 3 = 0 ; 4– 0,2x = 0
b)Hãy giải các phương trình bậc nhất một ẩn có ở câu a) ?
a) PT bậc nhất một ẩn là: x-2=0; 4-0,2x=0
b) Giải:
x-2=0 (*)
⟺ x=-2
Vậy tập nghiệm của pt (*) là S={-2}
4-0,2x=0 (**)
⟺-0,2x=-4
⟺x=-4/-0,2=20
Vậy tập nghiệm của pt (**) là S={20}
Đúng 0
Bình luận (0)
Các bạn ơi cho mình hoi Câu 1. Có phải bình phương thiếu lớn hơn hoặc bằng 0 ạ. Chứng minh tại sao. Và làm sao để biết đó là bình phương thiếu
bình phương thiếu của 1 tổng là \(a^2+ab+b^2\)
bình phương thiếu của 1 hiệu là \(a^2-ab+b^2\)
Chứng minh \(a^2+ab+b^2\ge0\)
Ta có: \(a^2+ab+b^2=a^2+2.a.\dfrac{1}{2}b+\left(\dfrac{1}{2}b\right)^2+\dfrac{3}{4}b^2\)
\(=\left(a+\dfrac{1}{2}b\right)^2+\dfrac{3}{4}b^2\ge0\)
Tương tự cho trường hợp còn lại
Đúng 1
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m.
3 x + 4 m = 4 x - 7 m
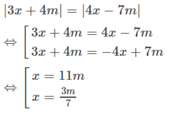
Vậy phương trình đã cho có hai nghiệm x = 11m và x = 3m/7 với mọi giá trị của m.
Đúng 0
Bình luận (0)
mình nhờ các bạn giải hộ vài bài với, mình xin cảm ơn rất nhiều
1. Giải phương trình
a) (x+5)(2x+1) - x2 + 25 = 0
b 3x/x-2 - x/x-5 + 3x/(x-2)(x-5) = 0
2 cho phương trình ẩn x
x+1/x+2+m = x+1/x+2-m
a) giải phương trình khi m = -3
b) tìm các giá trị m sao cho phương trình nhận x=3 làm nghiệm
1/a/\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=-6\end{cases}}}\)
Vậy ...................
b/ ĐKXĐ:\(x\ne2;x\ne5\)
.....\(\Rightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x^2-10x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\left(nhận\right)\\x=5\left(loại\right)\end{cases}}}\)
Vậy ..............
Đúng 0
Bình luận (0)
`Answer:`
`1.`
a. \(\left(x+5\right)\left(2x+1\right)-x^2+25=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x^2-25\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1\right)-\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(2x+1-x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-6\\x=-5\end{cases}}}\)
b. \(\frac{3x}{x-2}-\frac{x}{x-5}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\left(ĐKXĐ:x\ne2;x\ne5\right)\)
\(\Leftrightarrow\frac{3x\left(x-5\right)}{\left(x-2\right)\left(x-5\right)}-\frac{x\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}+\frac{3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\frac{3x\left(x-5\right)-x\left(x-2\right)+3x}{\left(x-2\right)\left(x-5\right)}=0\)
\(\Leftrightarrow3x\left(x-5\right)-x\left(x-2\right)+3x=0\)
\(\Leftrightarrow3x^2-15x-x^2+2x+3x=0\)
\(\Leftrightarrow2x\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\x=5\text{(Không thoả mãn)}\end{cases}}}\)
`2.`
\(ĐKXĐ:x\ne-m-2;x\ne m-2\)
Ta có: \(\frac{x+1}{x+2+m}=\frac{x+1}{x+2-m}\left(1\right)\)
a. Khi `m=-3` phương trình `(1)` sẽ trở thành: \(\frac{x+1}{x-1}=\frac{x+1}{x+5}\left(x\ne1;x\ne-5\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\\frac{1}{x-1}=\frac{1}{x+5}\end{cases}\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-1=x+5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\-1=5\text{(Vô nghiệm)}\end{cases}}}\)
b. Để phương trình `(1)` nhận `x=3` làm nghiệm thì
\(\Leftrightarrow\hept{\begin{cases}\frac{3+1}{3+2-m}=\frac{3+1}{3+2-m}\\3\ne-m-2\\3\ne m-2\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{4}{5+m}=\frac{4}{5-m}\\m\ne\pm5\end{cases}}\Leftrightarrow\hept{\begin{cases}5+m=5-m\\m\ne\pm5\end{cases}}\Leftrightarrow m=0\)