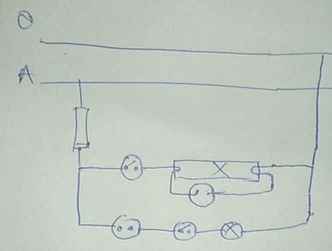
Mọi người ơi giải giúp e với!! Em cần gấp lắm ạ, e cảm ơn nhiều 🙇

Những câu hỏi liên quan
Mọi người ơi giúp em giải bài này với em cần gấp lắm, em cảm ơn trc vì đã giúp e ạ!!
Mọi người ơi giúp e giải bài này với ạ, huheoo e cần gấp lắm!! Thầy e cho nhìu bài tập quá làm ko kịp!!Em cảm ơn trước ạ.
Mọi người ơi, có thể giúp em giải bài này được không ạ. Em cần gấp lắm ạ.Em cảm ơn rất nhiều ạ.
a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2
Đúng 0
Bình luận (0)
Mọi người ơi, giúp em nhanh bài này với ạ, em đang cần gấp lắm ạ. Em cảm ơn rất nhiều ạ!!!!!

Mọi người giải giúp em bài này với ạ. Em cần gấp lắm ạ. Cảm ơn mọi người nhiều
vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )
Đúng 3
Bình luận (2)
em ơi chụp cả cái mạch điện a xem nào sao chụp nó bị mất r
Đúng 1
Bình luận (1)
Mọi người ơi làm giúp e với e cần gấp, em cảm ơn nhiều.
60B 61C 62C 63A 64B 65D 66D 67B 68A 69A 70A 71D 72D
Đúng 6
Bình luận (0)
60B 61C 62C 63A 64B 65D 66D 67B 68A 69A 70A 71D 72D
Đúng 1
Bình luận (0)

mọi người ơi giúp e đc không ạ! E thực sự đang cần gấp. E cảm ơn mọi người nhiều ạ!
\(5,\\ a,=x^4+4x^2+4-4x^2=\left(x^2+2\right)^2-4x^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\\ b,=x^4+16x^2+64-16x^2=\left(x^2+8\right)^2-16x^2=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\\ c,=x^8+x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x-x+1\\ =x^6\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^6-x^4+x^3-x+1\right)\left(x^2+x+1\right)\)
Đúng 3
Bình luận (1)
\(d,=x^8+2x^4+1-x^4=\left(x^4+1\right)^2-x^4=\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ =\left(x^4-x^2+1\right)\left(x^4+2x^2+1-x^2\right)\\ =\left(x^4-x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\\ e,=x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+1\\ =x^3\left(x^2+x+1\right)-x^2\left(x^2+x+x\right)+\left(x^2+x+1\right)\\ =\left(x^3-x^2+1\right)\left(x^2+x+1\right)\\ f,=x^3+2x^2-x^2-2x+2x+4\\ =\left(x+2\right)\left(x^2-x+2\right)\\ g,=x^4+2x^2+1-25=\left(x^2+1\right)^2-25\\ =\left(x^2+1-5\right)\left(x^2-1-5\right)=\left(x^2-4\right)\left(x^2-6\right)=\left(x-2\right)\left(x+2\right)\left(x^2-6\right)\)
\(h,=x^3-2x^2+2x^2-4x+2x-4=\left(x-2\right)\left(x^2+2x+2\right)\\ i,=a^4-4a^2b^2+4b^4-4a^2b^2=\left(a^2-2b^2\right)^2-4a^2b^2\\ =\left(a^2-2ab-2b^2\right)\left(a^2+2ab-2b^2\right)\)
Đúng 3
Bình luận (1)
Anh chị ơi giúp em làm bài này với ạ! E đg cần gấp lắm luôn ý:(( E cảm ơn anh chị nhiều ạ<3

\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)
Đúng 2
Bình luận (1)
Bào quan riboxom trong chất tế bào có chức năng gì?
Đúng 0
Bình luận (0)
a) \(=\left(x^2+x\right)+\left(4x+4\right)=x\left(x+1\right)+4\left(x+1\right)=\left(x+1\right)\left(x+4\right)\)
b) \(=\left(x^2+2x\right)-\left(3x+6\right)=x\left(x+2\right)-3\left(x+2\right)=\left(x+2\right)\left(x-3\right)\)
c) \(=\left(x^2-2x\right)-\left(3x-6\right)=x\left(x-2\right)-3\left(x-2\right)=\left(x-2\right)\left(x-3\right)\)
d) \(3x^2+9x-30=3\left(x^2+3x-10\right)=3\left[\left(x^2+5x\right)-\left(2x+10\right)\right]=3\left[x\left(x+5\right)-2\left(x+5\right)\right]=3\left(x-2\right)\left(x+5\right)\)
e) \(=-\left(3x^2-5x-2\right)=-\left[\left(3x^2-6x\right)+\left(x-2\right)\right]=-\left[3x\left(x-2\right)+\left(x-2\right)\right]=-\left(3x+1\right)\left(x-2\right)\)
f) \(x^2-7x+6=\left(x^2-x\right)-\left(6x-6\right)=x\left(x-1\right)-6\left(x-1\right)=\left(x-1\right)\left(x-6\right)\)
h) \(=4\left(x^2-9x+14\right)=4\left[\left(x^2-7x\right)-\left(2x-14\right)\right]=4\left[x\left(x-7\right)-2\left(x-7\right)\right]=4\left(x-2\right)\left(x-7\right)\)
i) \(=3\left(3x^2-8x+5\right)=3\left[\left(3x^2-3x\right)-\left(5x-5\right)\right]=3\left[3x\left(x-1\right)-5\left(x-1\right)\right]=3\left(x-1\right)\left(3x-5\right)\)
k) \(=-\left(2x^2+5x+2\right)=-\left[\left(2x^2+4x\right)+\left(x+2\right)\right]=-\left[2x\left(x+2\right)+\left(x+2\right)\right]=-\left(x+2\right)\left(2x+1\right)\)
l) \(=\left(x^2-5xy\right)-\left(2xy-10y^2\right)=x\left(x-5y\right)-2y\left(x-5y\right)=\left(x-5y\right)\left(x-2y\right)\)
m) \(=\left(x^2-2xy\right)-\left(xy-2y^2\right)=x\left(x-2y\right)-y\left(x-2y\right)=\left(x-2y\right)\left(x-y\right)\)
n) \(=\left(x^2-3xy\right)+\left(xy-3y^2\right)=x\left(x-3y\right)+y\left(x-3y\right)=\left(x+y\right)\left(x-3y\right)\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Mọi người giúp em với ạ, nếu đc thù em xin cả cách giải, em đang cần gấp lắm ạ, cảm ơn mọi người nhiều


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B
Đúng 1
Bình luận (0)