GIÚP MÌNH CÂU E VÀ F VỚI 

Những câu hỏi liên quan
Giúp mình với câu D, e, f bài 1 với bài 2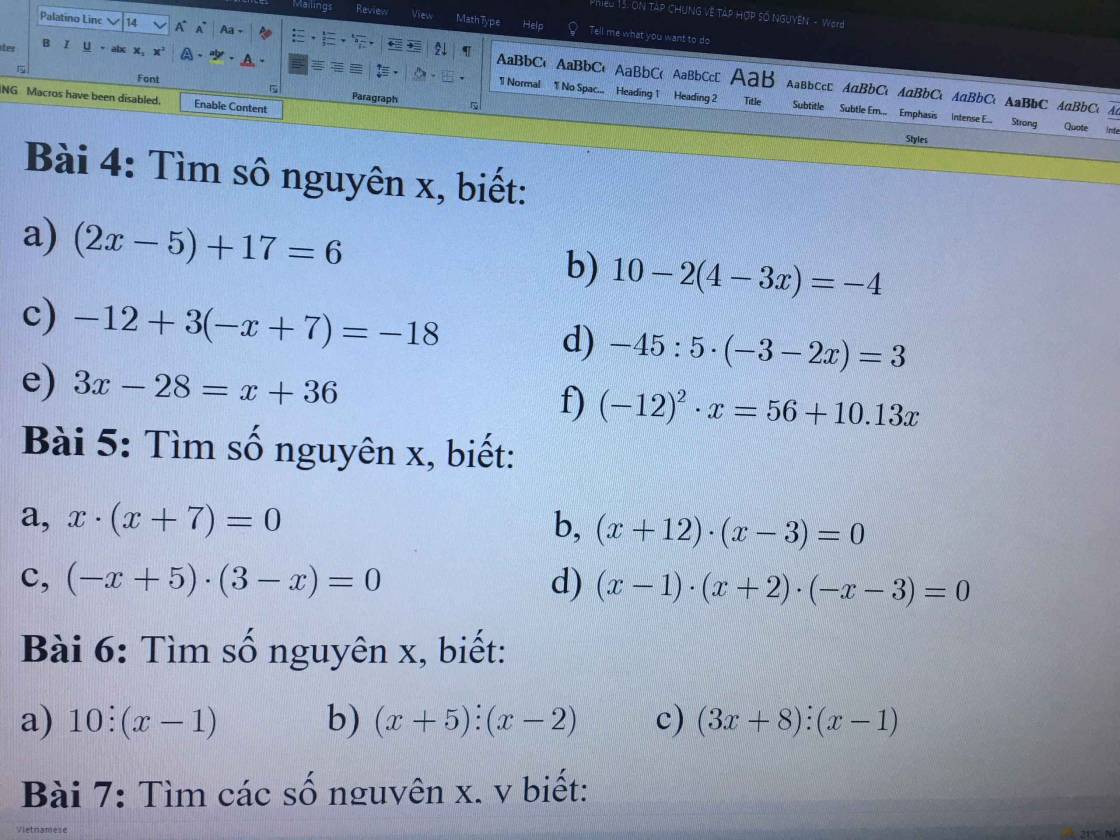
Xem thêm câu trả lời
HELP giúp mình với câu này mình khó làm quá Câu 3 : cho đường tròn tâm O đường kính AB . Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ) . Lấy điểm E trên cung nhỏ BC ( E khác B và C ) , AE cắt CD tại F Chứng minh : A) BEFI là tứ giác nội tiếp đường tròn B) AE . AF = AC . AD
a: góc AEB=1/2*180=90 độ
góc BEF+góc BIF=180 độ
=>BEFI nội tiếp
b: Xét ΔACF và ΔAEC có
góc ACF=góc AEC
góc CAF chung
=>ΔACF đồng dạng với ΔAEC
=>AC^2=AF*AE=AC*AD
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A=60, các đường phân BD và Ce cắt nhau tại I. Qua E kẻ đường thẳng vuông góc với BD, cắt BC ở F. CMR:
a/ E và F đối xứng nhau qua BD
b/ IF là tia phân giác góc BIC
c/ D và F đối xứng nhau qua IC
Ai giải giúp mình câu b mình tick cho nhé, câu a và c mình giải ra rồi
Cho tam giác DEF; có D=90 độ; E= 2.F. Tính E và F ( giúp mình với)
Ta có: \(D+E+F=180^0\)
mà \(D=90^0\)
\(\Rightarrow E+F=90^0\)
Ta lại có: \(E=2F\)
\(\Rightarrow3F=90^0\)
\(\Rightarrow F=30^0\)
\(\Rightarrow E=30^0.2=60^0\)
Đúng 0
Bình luận (1)
Cho đoạn thẳng AB có C là trung điểm của đoạn thẳng đó.Gọi D là trung điểm của BC.Biết BD3 cma) Vẽ hình và tính ABb) Vẽ E nằm trên tia đối của AB.Lấy điểm F nằm giữa hai điểm A,E và điểm H nằm giữa hai điểm E,F sao cho HA HE và cho biết HF1/2(HA-HE).Chứng tỏ rằng F là trung điểm của AE( Lưu ý: Bạn nào giải giúp mình thì xin vẽ giùm mình luôn cái hình.Không cần giải giúp mình câu a) mà giải giúp mình câu b).Thanks
Đọc tiếp
Cho đoạn thẳng AB có C là trung điểm của đoạn thẳng đó.Gọi D là trung điểm của BC.Biết BD=3 cm
a) Vẽ hình và tính AB
b) Vẽ E nằm trên tia đối của AB.Lấy điểm F nằm giữa hai điểm A,E và điểm H nằm giữa hai điểm E,F sao cho HA >HE và cho biết HF=1/2(HA-HE).Chứng tỏ rằng F là trung điểm của AE
( Lưu ý: Bạn nào giải giúp mình thì xin vẽ giùm mình luôn cái hình.Không cần giải giúp mình câu a) mà giải giúp mình câu b).Thanks
Làm giúp mình câu b và câu f với ạ. Mình cần gấp, mình cảm ơn trước
Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
Đúng 1
Bình luận (0)
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(=100\cdot\dfrac{\sqrt{3}}{3}\)
\(=\dfrac{100\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=100^2+\left(\dfrac{100\sqrt{3}}{3}\right)^2=\dfrac{40000}{3}\)
hay \(AC=\dfrac{200\sqrt{3}}{3}\left(cm\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời

giúp mình câu E,F,H
\(E=\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}\)
\(=\sqrt{9-2.3\sqrt{3}+3}+\sqrt{12-2.3.2\sqrt{3}+9}\)
\(=\sqrt{\left(9-3\right)^2}+\sqrt{\left(12-9\right)^2}\)
\(=\sqrt{6^2}+\sqrt{3^2}\)
\(=6+3=9\)
Đúng 0
Bình luận (0)
e) Ta có: \(E=\sqrt{12-6\sqrt{3}}+\sqrt{21-12\sqrt{3}}\)
\(=3-\sqrt{3}+2\sqrt{3}-3\)
\(=\sqrt{3}\)
f) Ta có: \(F=\sqrt{21-12\sqrt{3}}+\sqrt{21+12\sqrt{3}}\)
\(=2\sqrt{3}-3+2\sqrt{3}+3\)
\(=4\sqrt{3}\)
h) Ta có: \(H=\sqrt{14+6\sqrt{5}}+\sqrt{14-6\sqrt{5}}\)
\(=3+\sqrt{5}+3-\sqrt{5}\)
=6
Đúng 0
Bình luận (0)
\(F=\sqrt{21-12\sqrt{3}}+\sqrt{21+12\sqrt{3}}\)
\(=\sqrt{12-2.3.2\sqrt{3}+9}+\sqrt{12+2.3.2\sqrt{3}+9}\)
\(=\sqrt{\left(12-9\right)^2}+\sqrt{\left(12+9\right)^2}\)
\(=\sqrt{3^2}+\sqrt{21^2}\)
\(=3+21=24\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC có góc A=60, các đường phân BD và Ce cắt nhau tại I. Qua E kẻ đường thẳng vuông góc với BD, cắt BC ở F. CMR:
a/ E và F đối xứng nhau qua BD
b/ IF là tia phân giác góc BIC
c/ D và F đối xứng nhau qua IC
Ai giải giúp mình câu b với
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
Đúng 4
Bình luận (0)




















