5 và 12 nha bạn ơi. bộ ba pytago chứ mình không biết làm.

Gọi một cạnh góc vuông là x (x>0)
=> cạnh còn lại là : 17 - x
=> Phương trình theo định lý Py-ta-go là :
x^2 + (17 - x)^2 = 13^2
<=> x^2 + 289 - 34x + x^2 = 169
<=> 2x^2 - 34x + 120 = 0
<=> 2x^2 - 10x - 24x + 120 = 0
<=> 2x(x - 5) - 24(x - 5) = 0
<=> (2x - 24) = 0 hoặc x - 5 = 0
=> x = 12 hoặc x = 5
Vậy độ dài 2 cạnh góc vuông là : 12 cm và 5 cm
hoặc : 5 cm và 12 cm

Bài 8: Vì em nhắn tin nhờ cô giảng bài 8 nên cô chỉ giảng bài 8 thôi nhé

Gọi các cạnh góc vuông, cạnh huyền của tam giác cần tìm lần lượt là: a; b; c

Theo bài ra ta có: a+b+c =36; \(\dfrac{a}{b}\) = \(\dfrac{3}{4}\)

\(\dfrac{a}{b}\) = \(\dfrac{3}{4}\) ⇒ \(\dfrac{a}{3}\) = \(\dfrac{b}{4}\) ⇒ \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{a^2+b^2}{9+16}\) (1)

Vì tam giác vuông nên ta theo pytago ta có: a² + b²  = c² (2)

Thay (2) vào (1) ta có: \(\dfrac{a^2}{9}\) = \(\dfrac{b^2}{16}\) = \(\dfrac{c^2}{25}\)

⇒ \(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) = \(\dfrac{a+b+c}{3+4+5}\) = \(\dfrac{36}{12}\) = 3

a = 3.3 = 9 (cm)

b = 3.4 = 12 (cm)

c = 3.5 = 15 (cm)

Kết luận: độ dài cạnh bé của góc vuông là: 9 cm

               dộ dài cạnh lớn của góc vuông là 12 cm

              độ dài cạnh huyền là 15 cm

Bài 9:

a,Gọi độ dài cạnh góc vuông là: a

Theo pytago ta có: a² + a² = 2² = 4 ⇒ 2a² = 4 ⇒ a² = 2 ⇒ a = \(\sqrt{2}\)

b, Gọi độ dài cạnh góc vuông là :b 

Theo pytago ta có:

b² + b² = 10² =100 ⇒ 2b² = 100 ⇒ b² = 50⇒ b = 5\(\sqrt{2}\)

Bài 8 cô làm rồi nhé. 

Bài 10 ; Gọi độ dài các cạnh góc của tam giác vuông lần lượt là:

a; b theo bài ra ta có: 

\(\dfrac{a}{5}\) = \(\dfrac{b}{12}\) \(\Rightarrow\) \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{a^2+b^2}{25+144}\) (1)

Theo pytago ta có: a² + b² = 52² = 2704 (2)

Thay (2) vào (1) ta có: \(\dfrac{a^2}{25}\) = \(\dfrac{b^2}{144}\) = \(\dfrac{2704}{169}\) = 16

⇒ a² = 25.16 = (4.5)² ⇒ a = 20

b² = 144.16 = (12.4)² ⇒ b = 48

Bài 11 

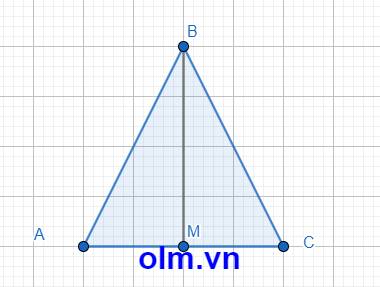
AM = \(\dfrac{1}{2}\) AC ( vì M là trung điểm AC)

AM = 16 \(\times\) \(\dfrac{1}{2}\) = 8 (cm)

BM \(\perp\)AC ( vì trong tam giác cân đường trung tuyến cũng là đường cao, đường trung trực)

⇒\(\Delta\)MAB vuông tại M

Xét tam giác vuông MAB theo pytago ta có:

AB² = AM² + BM²

⇒ BM² = AM² - AM²  = 17² - 8² = 225

    BM = \(\sqrt{225}\) cm = 15 cm

Kết luận BM = 15 cm

Gọi 2 cạnh góc vuông là a, b (cm; a,b >0)

Ta có: \(\left\{{}\begin{matrix}a+b=17\left(1\right)\\a^2+b^2=13^2=169\left(Pytago\right)\left(2\right)\end{matrix}\right.\)

(1) <=> (a+b)² = 289

<=> 2ab = 120

<=> ab = 60

<=> \(S=\dfrac{ab}{2}=\dfrac{60}{2}=30\left(cm^2\right)\)

Đặt tên cho \(\Delta\) này là \(\Delta\)ABC, ta có:

AB & BC là cạnh góc vuông.

AC là cạnh huyền.

Áp dụng định lý py-ta-go vào \(\Delta\)ABC, ta có:

AC² = AB² + BC²

13² = 12² + BC²

169 = 144 + BC²

BC² = 169 - 144 = 25

BC = \(\sqrt{25}\) = 5cm.

Vậy cạnh BC = 5cm hay cạnh góc vuông còn lại của \(\Delta\) = 5cm.

Giả sử ∆ABC có , BC = 13cm, AC = 12cm

Theo định lý Pytago, ta có:

Suy ra:

Vậy AB = 5 (cm)

Đặt tam giác đó là tam giác ABC vuông tại A.

Và BC là cạnh huyền; AB và AC là cạnh góc vuông.

Ta có ABC vuông tại A.

nên BC²=AB²+AC²(định lý Pytago)

Do đó: 13²=12²+AC²

169=144+AC²

AC²=169-144=25

AC=5(cm)

Vậy cạnh góc vuông cần tìm có độ dài là 5cm.

Gọi độ dài cạnh góc vuông cần tìm là x

Xét tam giác trên ta có:

=> 8² + x² = 17²

     x² = 17² - 8² = 225 = 15²

=> x = 15 cm

Chu vi tam giác là:

   17 + 8 + 15 = 40 (cm)

Đặt độ dài 2 cạnh góc vuông của tam giác đó là a và b; độ dài cạnh huyền là c (a,b,c > 0)

Diện tích của tam giác đó là \(\frac{ab}{2}=14\)(cm²) \(\Rightarrow ab=28\Leftrightarrow2ab=56\)(1)

Áp dụng ĐL Pytago ta có: \(a^2+b^2=c^2=13^2=169\)(2)

(1) + (2) \(\Rightarrow a^2+2ab+b^2=56+169=225\Leftrightarrow\left(a+b\right)^2=225\)

\(\Leftrightarrow a+b=\sqrt{225}=15\)(cm). Vậy ...

Đặt cạnh huyền của tam giác là x (\(x > 8\))

Theo giải thiết ta tính được cạnh góc vuông là \(x - 8\)

Áp dụng định lý Pitago ta tính được cạnh góc vuông còn lại là \(\sqrt {{x^2} - {{\left( {x - 8} \right)}^2}}  = \sqrt {16x - 64} \)

Ta có chu vi của tam giác là \(x + \left( {x - 8} \right) + \sqrt {16x - 64}  = 30\)

\(\begin{array}{l} \Leftrightarrow \sqrt {16x - 64}  = 38 - 2x\\ \Rightarrow 16x - 64 = {\left( {38 - 2x} \right)^2}\\ \Rightarrow 16x - 64 = 1444 - 152x + 4{x^2}\\ \Rightarrow 4{x^2} - 168x + 1508 = 0\end{array}\)

\( \Rightarrow x = 13\) và \(x = 29\)

Thay \(x = 13\) và \(x = 29\) vào phương trình \(\sqrt {16x - 64}  = 38 - 2x\) ta thấy chỉ có \(x = 13\) thảo mãn phương trình

Vậy cạnh huyền có độ dài là 13 cm.

Gọi 2 cạnh góc vuông và cạnh huyền lần lượt là a, b và c

Áp dụng định lí Pi-ta-go, ta có: \(a^2+b^2=c^2=169\)

Mặt khác a+b=17\(\Rightarrow\left(a+b\right)^2=289\Leftrightarrow a^2+b^2+2ab=289\Leftrightarrow169+2ab=289\Rightarrow ab=60\)

\(\Rightarrow S_{\Delta}=\frac{ab}{2}=\frac{60}{2}=30\)