Cho tam giác ABC có góc A = 90 độ. Lấy điểm D trên cạnh AB, lấy E trên cạnh AC. Chứng minh DE < BC.

Những câu hỏi liên quan
Cho tam giác ABC có góc A = 90 độ .Trên cạnh AB,AC lần lượt lấy điểm D,E
Chứng minh DE < BC
Cho tam giác ABC có góc A = 90 độ .Trên cạnh AB,AC lần lượt lấy điểm D,E
Chứng minh DE < BC
Nối D và C ta có : E , AC lần lượt là hình chiếu của các hình xiên DE,DC trên đường thẳng AC
Mà AE < AC ( vì E thuộc cạnh AC )
=> DE < DC ( quan hệ giữa đường xiên và hình chiếu của nó )
Mặt khác : AD ;AB lần lượt là hình chiếu của các đường xiên DC,BC trên đường thẳng AB mà AD < AB ( D thuộc cạnh AB )
=> DC < BC ( quan hệ giữa đường xiên và hình chiếu của nó )
Ta có : DE < DC ; DC < BC => DE < BC ( đpcm )
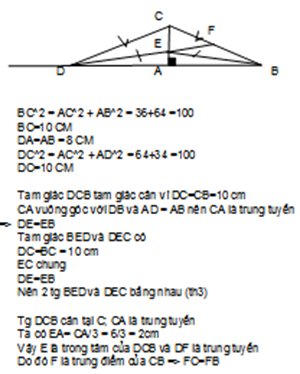
Tam giác ABC có góc A=90°; AB=8cm; AC=6cm. Trên cạnh AC lấy E biết AE=2cm. Trên tia đối của tia AB lấy điểm D sao cho AD=AB.
a) Tính BC.
b) Chứng minh tam giác BEC = tam giác DEC
c) Chứng minh DE đi qua trung điểm của cạnh BC.
Cho tam giác ABC có góc A = 90 0 , AB = 8cm, AC = 6cm .
a) Tính BC
b) Trên cạnh AC lấy điểm E sao cho AE = 2cm; trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ∆BEC = ∆DEC .
c) Chứng minh DE đi qua trung điểm cạnh BC
AEAC=26=13AEAC=26=13 (AE = 2cm, AC = 6cm)
=> E là trọng tâm ΔΔBCD (dhnb)
=> DE là trung tuyến ΔΔBCD (ĐN trọng tâm)
=> DE đi qua trung điểm của BC (ĐN trung tuyến)
Đúng 2
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=8^2+6^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông góc tại A trên cạnh BC lấy điểm E sao cho BE=BA. Tia phjan6 giác của góc B cắt AC tại D
a/ Chứng minh tam giác ABD =tam giác EBD
b/ DE vuông góc BC
c/ trên tia đối của tia AC lấy điểm M sao cho AM=AB trên cạnh AB lấy điểm N sao cho AN = AD. Chứng minh tam giác ABD=tam giác AMN
d/ gọi H là trung điểm MN , K là trung điểm BD . Chứng minh góc HAK = 90 độ
cho tam giác ABC có A =90 độ , AB =8cm , AC = 6cm
a,tính BC
b, trên cạnh AC lấy diểm E SAO CHO AE=2cm ; trên tia đối của tia AB lấy điểm D sao cho AD=AB . chứng minh tam giác BEC = tam giác DEC
CHỨNG MINH DE đi qua trung điểm cạnh BC
Cho tam giác ABC có góc A = 90 độ; AB=8cm; AC=6cm.
a, Tính BC
b, Trên AC lấy E sao cho AE= 2cm; trên tia đối của AB lấy D sao cho AD = AB. Chứng minh: Tam giác BEC = Tam giác DEC.
c, CM: DE đi qua trung điểm cạnh BC
Cho tam giác ABC có góc A tù. Trên cạnh AB lấy điểm D (khác A và B), trên cạnh AC lấy điểm E (khác A và C). Chứng minh rằng DE < BC.
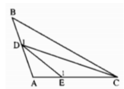
+ ΔADE có ∠E1 là góc ngoài ⇒ ∠E1 > ∠A
Mà ∠A > 90o ⇒ ∠E1 > 90o
ΔCDE có ∠E1 tù ⇒ CD là cạnh lớn nhất ⇒ CD > DE (1)
+ Tương tự xét ΔADC có ∠D1 là góc ngoài
⇒ ∠D1 > ∠A ⇒ ∠D1 > 90o (vì ∠A > 90º)
ΔBDC có ∠D1 tù ⇒ BC là cạnh lớn nhất ⇒ BC > CD (2)
Từ (1) và (2) suy ra BC > DE.
Đúng 0
Bình luận (0)
Cho tam giác ABC, góc A=90 độ và AB<AC.Trên cạnh AC lấy điểm D sao cho AD=AB. Trên tia AD lấy điểm E sao cho AE=AC.
a) Chứng minh: DE=BC
b) Chứng minh DE vuông góc với BC
c) Biết 4 lần góc B = 5 lần góc C. Tính góc AED.