BD với BC là 1 sao lại "Từ A vẽ đường  vuông góc với BD cắt nhau tại Hvà cắt BC tại E" vậy bạn ?????  

tuổi con HN là :

50 : ( 1 + 4 ) = 10 ( tuổi )

tuổi bố HN là :

50 - 10 = 40 ( tuổi )

hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi

ta có sơ đồ : bố : |----|----|----|

                  con : |----| hiệu 30 tuổi

tuổi con khi đó là :

 30 : ( 3 - 1 ) = 15 ( tuổi )

số năm mà bố gấp 3 tuổi con là :

 15 - 10 = 5 ( năm )

       ĐS : 5 năm

mình nha

giúp mình bài áy tớ sẽ k cho 10 cái luôn

Xét tam giác ABC có BC 2=AB 2+AC 2( Định lý Py-ta-go) Thay số:BC 2=6 2+8 2 BC 2=36+64=100 =>BC=10(cm) b) Vì BI là phân giác => góc ABI= góc HBI= góc ABC / 2 Xét tam giác ABI vuông tại A và tam giác HBI vuông tại H có: Bi chung, góc ABI= góc HBI ( cmt) => tam giác ABI= tam giác HBI (cạnh huyền - góc nhọn) c)Gọi giao của AH và BI là K Vì tam giác ABI=tam giác HBI (cmt)=> AB=HB( 2 cạnh tương ứng) Xét tam giác AKB và tam giác HKB có: AB=HB (cmt) góc ABK=góc HBK(cmt) BK chung =. tam giác AKB= tam giác HKB ( c.g.c) => KB=KH ( 2 cạnh tương ứng) => K là trung điểm của BH (1) Vì AB=HB (cmt) => tam giác ABH cân tại B=> AH là đường cao của tam giác ABH=> AH vuông góc với BK hay AH vuông góc với BI(2) Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AH 

Xét tam giác ABC có BC 2=AB 2+AC 2( Định lý Py-ta-go) Thay số:BC 2=6 2+8 2 BC 2=36+64=100 =>BC=10(cm) b) Vì BI là phân giác => góc ABI= góc HBI= góc ABC / 2 Xét tam giác ABI vuông tại A và tam giác HBI vuông tại H có: Bi chung, góc ABI= góc HBI ( cmt) => tam giác ABI= tam giác HBI (cạnh huyền - góc nhọn) c)Gọi giao của AH và BI là K Vì tam giác ABI=tam giác HBI (cmt)=> AB=HB( 2 cạnh tương ứng) Xét tam giác AKB và tam giác HKB có: AB=HB (cmt) góc ABK=góc HBK(cmt) BK chung =. tam giác AKB= tam giác HKB ( c.g.c) => KB=KH ( 2 cạnh tương ứng) => K là trung điểm của BH (1) Vì AB=HB (cmt) => tam giác ABH cân tại B=> AH là đường cao của tam giác ABH=> AH vuông góc với BK hay AH vuông góc với BI(2) Từ (1) và (2) => BI là đường trung trực của đoạn thẳng AH 

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)

Do tam giác ABC có

AB = 3 , AC = 4 , BC = 5

Suy ra ta được

(3*3)+(4*4)=5*5  ( định lý pi ta go) 

9 + 16 = 25

Theo định lý py ta go thì tam giác abc vuông tại A

a) Áp dụng định lý Pytago vào \(\Delta\)ABC có
AB²+AC²=BC²

thay AB=3cm, AC=4cm va BC=5cm, ta có:

3²+4²=5²

=> 9+16=25 (luôn đúng)

=> đpcm

b) có D nằm trên tia đối của tia AC

=> D,A,C thằng hàng và A nằm giữa D và C

=> DA+AC=DC

=> DA+4=6

=>DA=2(cm)

áp dụng định lý Pytago vào tam giác ABD vuông tại A có:

AB²+AD²=BD²

=> 3²+2²=BD²

=> 9+4=BD²

=> \(BD=\sqrt{13}\)(cm)

a)  Xét tam giác BHA và tam giác BAC có

góc BHA= góc BAC (=90)

góc B chung

=> tam giác BHA đồng dạng tam giác BAC (g.g)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

góc ABD=góc EBD

=>ΔBAD=ΔBED

b: Xét ΔDAN vuông tại A và ΔDEC vuông tại E có

DA=DE
góc ADN=góc EDC
=>ΔDAN=ΔDEC
=>AN=EC

c: BA+AN=BN

BE+EC=BC

mà BA=BE; AN=EC

nên BN=BC

=>ΔNBC cân tại B

mà BD là phân giác

nên BD vuôg góc NC

`a,` Xét Tam giác `BAE` và Tam giác `BIE` có:

`BA = BI (g``t)`

\(\widehat{ABE} =\widehat{IAE}\) (tia phân giác \(\widehat{ABI}\))

`AE` chung

`=>` Tam giác `BAE =` Tam giác `BIE (c-g-c)`

`b,` vì Tam giác `BAE =` Tam giác `BIE` (a)

`=>` \(\widehat{BAE}=\widehat{BIE}=90^0\) (2 góc tương ứng)

`=> \(EI\perp BC\) 

`c,` Xét Tam giác `BAH và` Tam giác `BIH`

`BA=BI (g``t)`

\(\widehat{BAH}=\widehat{BIH}\) (tia phân giác \(\widehat{ABI}\))

`AH` chung

`=>` Tam giác `BAH =` Tam giác `BIH (c-g-c)`

`=>` \(\widehat{BHA}=\widehat{BHI}\) (2 góc tương ứng)

mà 2 góc này ở vị trí kề bù

`=>`\(\widehat{BHA}+\widehat{BHI}=180^0\)

`=>` \(\widehat{BHA}=\widehat{BHI} =\) \(\dfrac{180}{2}=90^0\)

`=>` \(BE\perp AI\) (đpcm)

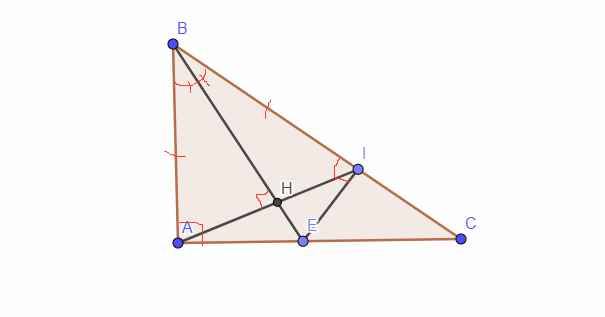
^{*Hình đây nha cậu, xl nãy làm bài mình quên gửi:').}

BÀI 1 cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E

a) chứng minh AB=EB

b) chứng minh tam giác BED vuông

c) DE cắt AB tại F, chứng minh AE//FC

BÀI 2 cho tam giác ABC cân tại A, có BD và CE là hai đường trung tuyến cắt nhau tại I

a) chứng minh tam giác IBC cân

b)lấy O thuộc tia IC sao cho IO=IE.Gọi K là trung điểm của IA.Chứng minh AO, BD, CK đồng quy

BÀI 3 cho tam giác ABC cân tại A, kẻ tia phân giác của góc BAC cắt BC tại H.Biết AB=15cm, BC=18cm

a)so sánh góc A và góc C

b)chứng minh rằng tam giác ABH = tam giác ACH

c)vẽ trung tuyến BD của tam giác ABC cắt AH tại G.Chứng minh rằng: tam giác AEG = tam giác ADG

d)tính độ dài AG

e) kẻ đường thẳng CG cắt AB ở E, chứng minh rằng: tam giác AEG = tam giác ADG

BÀI 4 cho tam giác ABC vuông tại A, trên BC lấy điểm D sao cho BA=BD.Qua D kẻ đường vuông góc với BC cắt AC tại E, qua C kẻ đường vuông góc với BE tại H cắt AB tại F

a)chứng minh tam giác ABE = tam giác DBE

b) chứng minh tam giác BCF cân

c) chứng minh 3 điểm F.D,E thẳng hàng

d)trên cạnh CB lấy điểm M sao cho CA=CM.Tính số đo góc DAM

BÀI 5 cho tam giác ABC cân tại A, kẻ BD vuông góc AC, kẻ CE vuông góc AB, BD và CE cắt nhau tại I

a)chứng minh rằng tam giác BDC = tam giác CEB

b)so sánh góc IBE và góc ICD

c) đường thẳng AI cắt BC tại H, chứng minh AI vuông góc BC tại H

BÀI 6 cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm

a)tính BC

b)trung trực của BC cắt AC tại D và cắt AB tại F, chứng minh góc DBC=DCB

c) trên tia đối của tia DB lấy E sao cho DE=DC, chứng minh tam giác BCE vuông và DF là phân giác góc ADE

d) chứng minh BE vuông góc FC

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
 => BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE. 
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
 =>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
 (Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của  ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE      => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực  Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/

(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
 => ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM          => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của  ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).