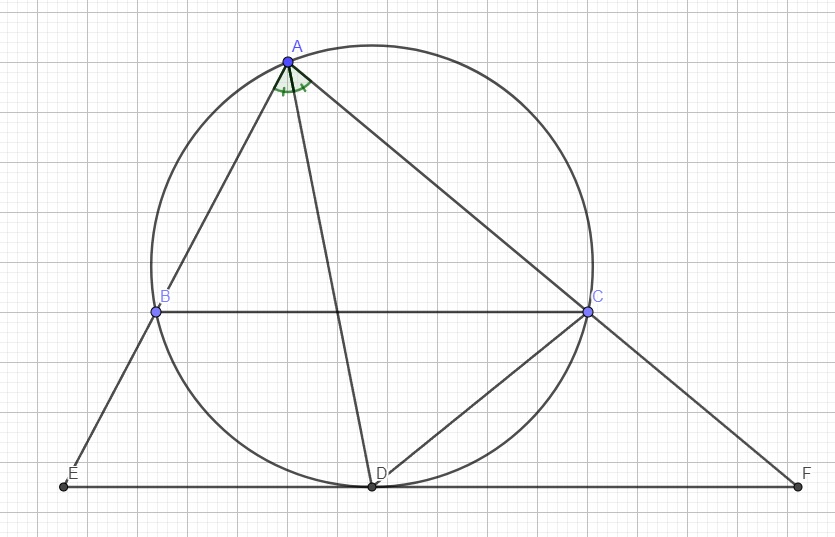
cho tam giác abc nội tiếp (O). phân giác EAF cắt đường tròn tại D. Tiếp tuyến tại D cắt tia AE ; AF tại B;C. chứng minh ef//bc

Những câu hỏi liên quan
cho tam giác abc nội tiếp (O). phân giác EAF cắt đường tròn tại D. Tiếp tuyến tại D cắt tia AE ; AF tại B;C. chứng minh ef//bc
Vì \(AD\) là tia phân giác \(\widehat{EAF}\) (giả thiết)
\(\Rightarrow\stackrel\frown{DE}=\stackrel\frown{DF}\)
\(\Rightarrow\widehat{EBD}=\widehat{FDE}\)
\(\Rightarrow EF//BC\)
Đúng 1
Bình luận (0)
Cho tam giác ABC nội tiếp (O). Tia phân giác góc A cắt BC tại D, cắt đường tròn tại E. Tiếp tuyến của đường tròn tại C cắt AE tại M. Qua E vẽ đường thằng song song với BC cắt CM tại N. Chứng minh : 1/DC +1/MC = 1/NC .
Cho tam giác ABC nội tiếp đường tròn(O), các tiếp tuyến B<C hau tại E, AE cvới (O) cắt đường tròn tại D. CMR tứ giác OBEC nội tiếp . Từ E kẻ đường thẳng d song song với tiếp tuyến A của đường tròn, d cắt AB,AC tại P,Q. CMR AC.AQ= AD.AE
Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến của (O) tại A cắt BC tại P.
a) Cm PA^2=PB.PC
b) Tia phân giác trong góc A cắt BC tại D và (O) tại M. Cm MB^2=MA.MD
a: Xét ΔPAC và ΔPBA có
\(\widehat{P}\) chung
\(\widehat{PAC}=\widehat{PBA}\)
Do đó:ΔPAC\(\sim\)ΔPBA
Suy ra: \(\dfrac{PA}{PB}=\dfrac{PC}{PA}\)
hay \(PA^2=PB\cdot PC\)
Đúng 0
Bình luận (0)
Bài 7: Cho tam giác ABC nội tiếp đường tròn (O). Phân giác góc BAC cắt BC tại D và cắt (O) tại M. Chứng minh BM là tiếp tuyến của đường tròn ngoại tiếp tam giác ABD.
cho tam giác ABC nội tiếp đường tròn (O,R). Phân giác góc BAC cắt BC tại D và cắt đường tròn (O) tại E.Vẽ đường tròn đường kính AE. Đường thẳng qua D vuông góc với AE cắt đường kinhs AE tại F. chứng minh tam giác EFC cân
Cho tam giác ABC cân tại A , nội tiếp đường tròn (O). Gọi D và H lần lượt là trúng điểm của AC và BC . Tiếp tuyến đường tròn (O) tại A cắt BD tại E , tia CE cắt đường tròn (O) tại F a, Chứg minh :BC//AE b, Chứg minh : tứ giác ABCE là hình bình hành c, Chứg minh: 4 điểm H,O,C,D cùng thuộc một đường tròn
a: Ta có: BC⊥AH
AH⊥AE
Do đó: BC//AE
Đúng 1
Bình luận (1)
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). D là trung điểm AB, tia CD cắt đường tròn (O) tại E. Kẻ CF//AE với F thuộc (O), ta EF cắt AC tại G. Chứng minh rằng BG là tiếp tuyến của đường tròn (O).
Cho ΔABC nội tiếp đường tròn (O). Tia phân giác của góc BAC cắt (O) tại D. Tiếp tuyến tại D cắt (O) cắt 2 đường thẳng AB, AC lần lượt tại E và F. Chứng minh: AB.AF = AC. AE = AD2
Ta có: \(\widehat{CDF}=\widehat{CAD}\) (cùng chắn AD)
\(\widehat{CAD}=\widehat{BAD}\) (AD là phân giác)
\(\widehat{BAD}=\widehat{BCD}\) (cùng chắn BD)
\(\Rightarrow\widehat{CDF}=\widehat{BCD}\)
\(\Rightarrow BC||EF\) (hai góc so le trong bằng nhau)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\Rightarrow AB.AF=AC.AE\)
Cũng từ BC song song EF \(\Rightarrow\widehat{ACB}=\widehat{AFD}\) (đồng vị)
Mà \(\widehat{ACB}=\widehat{ADB}\) (cùng chắn AB)
\(\Rightarrow\widehat{AFD}=\widehat{ADB}\)
Xét 2 tam giác AFD và ADB có:
\(\left\{{}\begin{matrix}\widehat{FAD}=\widehat{DAB}\left(\text{AD là phân giác}\right)\\\widehat{AFD}=\widehat{ADB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AFD\sim\Delta ADB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AF}{AD}\Rightarrow AB.AF=AD^2\)
\(\Rightarrow AB.AF=AC.AE=AD^2\)
Đúng 2
Bình luận (0)