LAM TINH CHIA:(x3+2x2-2x-1)/(x2+3x+1)

Những câu hỏi liên quan
Thực hiện phép tính:
a)(x4-3x-1):(x2-x-1)
b)(x3-x2+5x-4):(-x+2x2+1)
c)(2x2+2x-5x3+2x4-1):(-x+x2+1)
\(a,=\left[x^2\left(x^2-x-1\right)+x^3+x^2-3x-1\right]:\left(x^2-x-1\right)\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2x^2-2x-1\right]\\ =\left[x^2\left(x^2-x-1\right)+x\left(x^2-x-1\right)+2\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)\\ =\left[\left(x^2+x+2\right)\left(x^2-x-1\right)+1\right]:\left(x^2-x-1\right)=x^2+x+2R1\)
Đúng 2
Bình luận (0)
a)A=3x(2/3x2-3x4)+(3x2)(x3-1)+(-2+9).x2-12
b)B=x(2x3+x+2)-2x2(x2+1)+x2-2x+1
c)C=x.(2x+1)-x2(x+2)+x3-x+3
a, \(A=2x^3-9x^5+3x^5-3x^2+7x^2-12=-6x^5+2x^3+4x^2-12\)
b, \(B=2x^4+x^2+2x-2x^3-2x^2+x^2-2x+1=2x^4-2x^3+1\)
c, \(C=2x^2+x-x^3-2x^2+x^3-x+3=3\)
Đúng 1
Bình luận (0)
a) 3x(x+1)-x(3x+2)
b) 2x(x2-5x+6)+(x-1)(x+3)
c) (x2-xy+y2)-(x2+2xy+y2)
d) (2/5xy+x-y)-(3x+4y)-2/5xy
e) 2xy(x2-4xy+4y2)
f) (x+y)(xy+5)
g) (x3-2x2-x+2):(x-1)
h) (2x2+3x-2):(2x-1)
d. (3x2 – 6x) : (2 – x) e. (x3 + 2x2 – 2x – 1) : (x2 + 3x+1)
d: \(=\dfrac{3x\left(x-2\right)}{-\left(x-2\right)}=-3x\)
e: \(=\dfrac{x^3+3x^2+x-x^2-3x-1}{x^2+3x+1}=x-1\)
Đúng 0
Bình luận (0)
Giải phương trình :
1) √x2+x+2 + 1/x= 13-7x/2
2) x2 + 3x = √1-x + 1/4
3) ( x+3)√48-x2-8x= 28-x/ x+3
4) √-x2-2x +48= 28-x/x+3
5) 3x2 + 2(x-1)√2x2-3x +1= 5x + 2
6) 4x2 +(8x - 4)√x -1 = 3x+2√2x2 +5x-3
7) x3/ √16-x2 + x2 -16 = 0
Bài 1 Rút gọn biểu thứca, [(3x - 2)(x + 1) - (2x + 5)(x2 - 1)] : (x + 1)b, (2x + 1)2 - 2(2x + 1)(3 - x) + (3 - x)2c, (x - 1)2 - (x + 1) (x2 - x + 1) - (3x + 1)(1 - 3x)d, (x2 + 1)(x - 3) - (x - 3)(x2 + 3x + 9)e, (3x +2)2 + (3x - 2)2 - 2(3x + 2)(3x - 2) + xBài 2 Phân tích các đa thức sau thành nhân tử1, 3(x + 4) - x2 - 4x2, x2 - xy + x - y3, 4x2 -25 + (2x + 7)(5 - 2x)4, x2 + 4x - y2 + 45, x3 - x2 - x + 16, x3 + x2y - 4x - 4y7, x3 - 3x2 + 1 - 3x8, 2x2 + 3x - 59, x2 - 7xy + 10y210, x3 - 2x2 + x - xy...
Đọc tiếp
Bài 1 Rút gọn biểu thức
a, [(3x - 2)(x + 1) - (2x + 5)(x2 - 1)] : (x + 1)
b, (2x + 1)2 - 2(2x + 1)(3 - x) + (3 - x)2
c, (x - 1)2 - (x + 1) (x2 - x + 1) - (3x + 1)(1 - 3x)
d, (x2 + 1)(x - 3) - (x - 3)(x2 + 3x + 9)
e, (3x +2)2 + (3x - 2)2 - 2(3x + 2)(3x - 2) + x
Bài 2 Phân tích các đa thức sau thành nhân tử
1, 3(x + 4) - x2 - 4x
2, x2 - xy + x - y
3, 4x2 -25 + (2x + 7)(5 - 2x)
4, x2 + 4x - y2 + 4
5, x3 - x2 - x + 1
6, x3 + x2y - 4x - 4y
7, x3 - 3x2 + 1 - 3x
8, 2x2 + 3x - 5
9, x2 - 7xy + 10y2
10, x3 - 2x2 + x - xy2
Bài 2: Tínha) ( x4 - x3 + x2 + 3x ) : ( x2 - 2x + 3 )b) ( 21x2y3 ) : ( 6xy) c) x2- 36 : ( 2x + 10) ( 6 - x )d) 2x2 ( 3x - 5 )e) ( 12x3y + 18x2y) : 2xyg) ( x2 + 2x + 1 ) : ( x + 1 )h) 5y ( 2y - 1 ) - ( 3y + 2 ) ( 3 - 3y)i) ( 6x3 - x2 + 5x - 1 ) : ( 2x - 1 )
Đọc tiếp
Bài 2: Tính
a) ( x4 - x3 + x2 + 3x ) : ( x2 - 2x + 3 )
b) ( 21x2y3 ) : ( 6xy)
c) x2- 36 : ( 2x + 10) ( 6 - x )
d) 2x2 ( 3x - 5 )
e) ( 12x3y + 18x2y) : 2xy
g) ( x2 + 2x + 1 ) : ( x + 1 )
h) 5y ( 2y - 1 ) - ( 3y + 2 ) ( 3 - 3y)
i) ( 6x3 - x2 + 5x - 1 ) : ( 2x - 1 )
`@` `\text {Ans}`
`\downarrow`

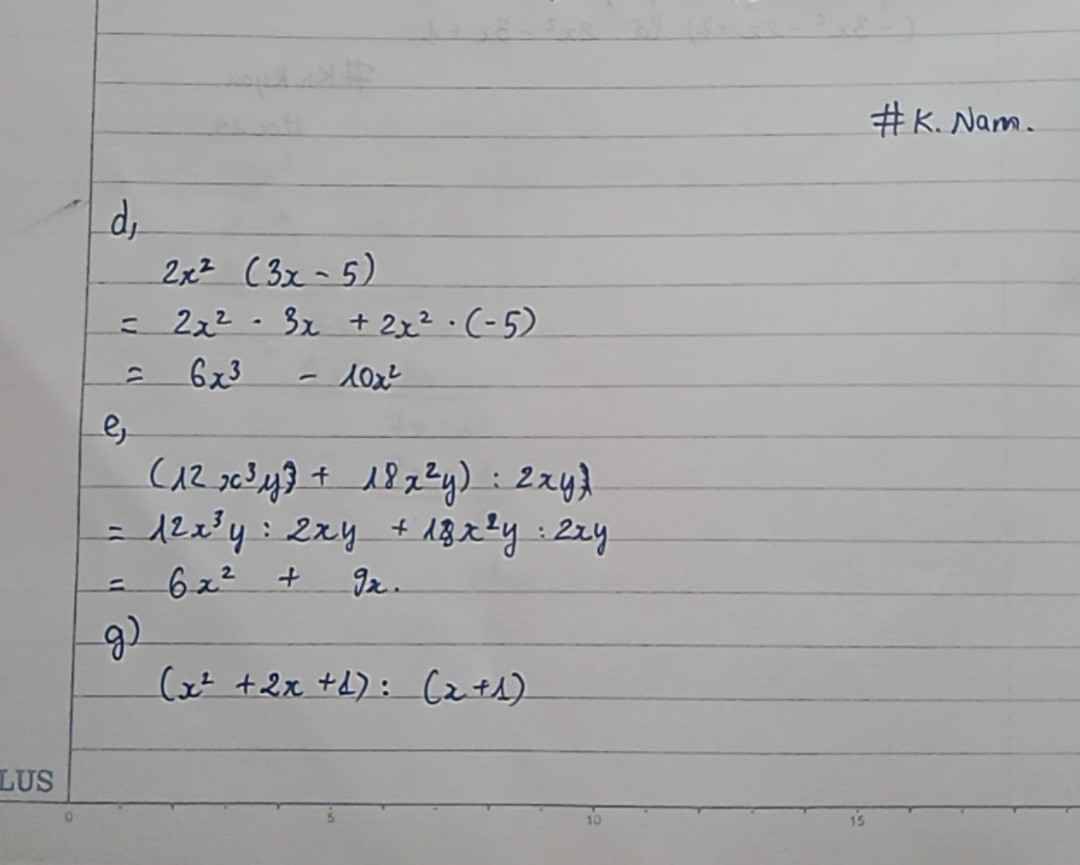

*Máy tớ cam hơi mờ, cậu thông cảm ._.*
Cậu viết lại rõ đề câu c, nhé.
Đúng 5
Bình luận (0)
1. (x3 – 3x2 + x – 3) : (x – 3) 2. (2x4 – 5x2 + x3 – 3 – 3x) : (x2 – 3) 3. (x – y – z)5 : (x – y – z)3 4. (x2 + 2x + x2 – 4) : (x + 2) 5. (2x3 + 5x2 – 2x + 3) : (2x2 – x + 1) 6. (2x3 – 5x2 + 6x – 15) : (2x – 5)
1: \(=x^2+1\)
3: \(=\left(x-y-z\right)^2\)
Đúng 1
Bình luận (0)
Bài 1: Khai triển các hằng đẳng thức.
1,(x+1)2
2,(2x+1)2
3, (2x+y)2
4, (2x+3)2
5, ( 3x+2y)2
6, (2x2+1)2
7, (x3+1)2
8, (x2+y3)2
9, ( x2+2y2)2
10, (1/2x+1/3y)2
1) \(\left(x+1\right)^2=x^2+2x+1\)
2) \(\left(2x+1\right)^2=4x^2+4x+1\)
3) \(\left(2x+y\right)^2=4x^2+4xy+y^2\)
4) \(\left(2x+3\right)^2=4x^2+12x+9\)
5) \(\left(3x+2y\right)^2=9x^2+12xy+4y^2\)
6) \(\left(2x^2+1\right)^2=4x^4+4x^2+1\)
7) \(\left(x^3+1\right)^2=x^6+2x^3+1\)
8) \(\left(x^2+y^3\right)^2=x^4+2x^2y^3+y^6\)
9) \(\left(x^2+2y^2\right)^2=x^4+4x^2y^2+4y^4\)
10) \(\left(\dfrac{1}{2}x+\dfrac{1}{3}y\right)^2=\dfrac{1}{4}x^2+\dfrac{1}{3}xy+\dfrac{1}{9}y^2\)
Đúng 1
Bình luận (0)





















