\(\frac{-3x+1}{2x+1}+2\le0\)

\(\frac{-3x+1+4x+2}{2x+1}\le0\)

\(\frac{x+3}{2x+1}\le0\)

Lập bảng xet dấu, chú ý các mốc x = -3, x = -1/2

Nghiệm bpt là \(-3\le x<-\frac{1}{2}\)

nhi thức là gì v?

ko bieets

Quy tắc xét dấu một nhị thức dựa trên định lí :

“Nhị thức f(x) = ax + b (a≠0) có dấu cùng với hệ số a khi x lấy giá trị trong khoảng và trái dấu với hệ số a khi x lấy các giá trị thuộc khoảng ”.

Áp dụng: Ta lập bảng xét dấu của vế trái f(x) của bất phương trình:

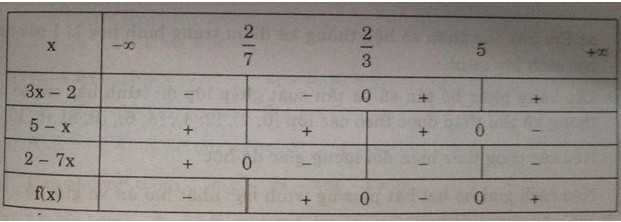
Tập nghiệm của bất phương trình:

\(\left(4A\right)\\ a,\\ \Leftrightarrow\left[\left(x-2\right)\left(2x+3\right)\right]\left[\left(x-2\right)\left(2x+3\right)\right]=0\\ \Leftrightarrow\left(-x-5\right)\left(3x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-x-5=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=\dfrac{-1}{3}\end{matrix}\right.\\ b,\\ \Leftrightarrow\left[3\left(2x+1\right)\right]^2-\left[2\left(x+1\right)\right]^2=0\\ \Leftrightarrow\left[3\left(2x+1\right)-2\left(x+1\right)\right]\left[3\left(2x+1\right)+2\left(x+1\right)\right]=0\\ \Leftrightarrow\left(4x+1\right)\left(8x+5\right)=0\) 

\(\Leftrightarrow\left[{}\begin{matrix}4x+1=0\\8x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{4}\\x=\dfrac{-5}{8}\end{matrix}\right.\\ c,\\ \Leftrightarrow\left[\left(x+1\right)+1\right]^2=0\\ \Leftrightarrow\left(x+1\right)+1=0\\ \Leftrightarrow x+2=0\Rightarrow x=-2\\ d,\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x+3\right)+\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left[\left(x-1\right)\left(x+3\right)+1\right]=0\\ \Leftrightarrow\left(x+3\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+3=0\\\left(x+2\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\) 

\(\left(4B\right)\\ a,\\ \Leftrightarrow49-14x+x^2-4\left(x+25\right)^2=0\\ \Leftrightarrow49-14x+x^2-4x^2-40x-100=0\\ \Leftrightarrow3x^2-54x-51=0\\ \Leftrightarrow-3\left(x^2+18x+17\right)=0\\ \Leftrightarrow\left(x+1\right)\left(x+17\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+17=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-17\end{matrix}\right.\\ b,\\ \Leftrightarrow4x^2\left(x^2-2x+1\right)-\left(4x^2+4x+1\right)=0\\ \Leftrightarrow x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\) 

\(c,\\ \Leftrightarrow\left(x+1\right)\left(x^2-x+1\right)=\left(x+1\right)\left(2-x\right)=0\\ \Leftrightarrow\left(x+1\right)\left[\left(x^2-x+1\right)-\left(2-x\right)\right]=0\\ \Leftrightarrow\left(x+1\right)\left(x^1-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\\x=-1\end{matrix}\right.\\ d,\\ \Leftrightarrow\left(x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)