Điểm N (0;0) trùng với gốc tọa độ . Đúng hay sai

Những câu hỏi liên quan
cho tam giác ABC , I là điểm thỏa mãn 2IA-IB+4IC=0, K là điểm thỏa mãn KA+2KB+3KC=0,P là điểm thỏa mãn PA+mPB+nPC=0
Trong các điểm sau: M(0; -1); N(1/3; -1/3); P(1/2; 0); Q(1/2; 1), điểm nào không thuộc đồ thị của hàm số y = 2x - 1 ?
A. điểm M B. điểm N C. điểm P D. điểm Q
cho đường tròn (0).đường thẳng d tiếp xúc với đường tròn (0)tại a.trên d lấy 1 điểm b(b≠a),vẽ đường tròn (b,ba)cắt đường tròn (0)tại điểm c (c≠a)chứng minh bc là tiếp tuyến của (0)
Trên 1 mặt phẳng hãy biểu diễn các điểm M (-3;2);N (4;-1);P (0;-5);Q (-1;4)
- Tìm các điểm nằm trong góc vuông thứ 3
- Tìm vị trí các điểm có tọa độ x, y thỏa mãn
Điểm E: x (y-3)=0
Điểm F : (x+3)y=0
Điểm H : |x-5|+|2y+6|=0
Điểm G :(x-1)2+(y+5)2=0
a: Không có điểm nào trong góc phần tư thứ III
b: Tọa độ điểm E là:
x=0và y-3=0
=>x=0và y=3
Tọa độ F là:
x+3=0 và y=0
=>F(-3;0)
Tọa độ H là:
x-5=0 và 2y+6=0
=>x=5 và y=-3
Tọa độ G là:
x-1=0 và y+5=0
=>x=1 và y=-5
Đúng 0
Bình luận (0)
Cho n điểm phân biệt trên mặt phẳng (n
∈
ℕ
, n 2). Số véctơ khác
0
⇀
có cả điểm đầu và điểm cuối là các điểm đã cho bằng A. n(n-1) B.
n
(
n
-
1
)
2
C. 2n(n-1) D. 2n
Đọc tiếp
Cho n điểm phân biệt trên mặt phẳng (n ∈ ℕ , n > 2). Số véctơ khác 0 ⇀ có cả điểm đầu và điểm cuối là các điểm đã cho bằng
A. n(n-1)
B. n ( n - 1 ) 2
C. 2n(n-1)
D. 2n
Chọn A
Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véc tơ đó là: ![]()
Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm. Nên số véctơ là:
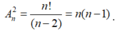
Đúng 0
Bình luận (0)
Viết phương trình tổng quát của đường thẳng đi qua điểm M(4; 0) và điểm N(0; -1).
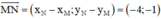
Đường thẳng MN nhận 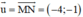 là 1 vtcp
là 1 vtcp
⇒ MN nhận 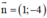 là 1 vtpt
là 1 vtpt
Mà M(4; 0) thuộc đường thẳng MN
⇒ Phương trình đường thẳng MN: 1(x - 4) – 4(y - 0) = 0 hay x – 4y – 4 = 0.
Đúng 0
Bình luận (0)
Cho điểm A(a;0), a>0. Điểm M di chuyển trên đoạn OA, điểm N di chuyển trên tia Oy sao cho AM=ON. Khi đó, trung trực của đoạn thẳng MN luôn đi qua điểm cố định I(x;y). Tìm giá trị biểu thức 2x-y?
Gọi \(M\left(m;0\right)\) với \(m\in\left[0;a\right]\) \(\Rightarrow AM=a-m\)
\(N\left(0;n\right)\Rightarrow ON=n\) \(\Rightarrow a-m=n\Rightarrow m+n=a\)
Phương trình trung trực MN đi qua \(\left(\frac{m}{2};\frac{a-m}{2}\right)\) và nhận \(\overrightarrow{NM}=\left(m;-n\right)=\left(m;m-a\right)\) là vtpt có dạng:
\(m\left(x-\frac{m}{2}\right)+\left(m-a\right)\left(y-\frac{a-m}{2}\right)=0\)
\(\Leftrightarrow mx-\frac{m^2}{2}+my-\frac{am-m^2}{2}-ay+\frac{a^2-am}{2}=0\)
\(\Leftrightarrow mx+my-ay-am+\frac{a^2}{2}=0\)
\(\Leftrightarrow m\left(x+y-a\right)+\left(-ay+\frac{a^2}{2}\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x+y-a=0\\-ay+\frac{a^2}{2}=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{a}{2}\\y=\frac{a}{2}\end{matrix}\right.\)
\(\Rightarrow\) Đường trung trực của MN luôn đi qua điểm cố định \(I\left(\frac{a}{2};\frac{a}{2}\right)\)
\(\Rightarrow2x-y=\frac{a}{2}\)
Đúng 0
Bình luận (0)
Tìm bán kính đường tròn đi qua 3 điểm A ( 0 ; 0 ) , B ( 0 ; 6 ) , C ( 8 ;0 ) .
Tam giác ABC vuông tại A \(\Rightarrow R=\frac{BC}{2}=\frac{1}{2}\sqrt{6^2+8^2}=5\)
Đúng 0
Bình luận (0)
Cho n điểm phân biệt. Hãy xác định số vecto khác vecto 0 có điểm đầu và điểm cuối thuộc n điểm trên?
Khi có n điểm, ta có n cách chọn điểm đầu và n-1 cách chọn điểm cuối. Nên ta sẽ có n(n-1) cách xác định số vecto khác 0 thuộc n điểm trên
Đúng 1
Bình luận (0)
26. Cho đg thẳng denta 7x +10y -150 . Trong các điểm M (1;-3) , N(0;4) , P(8;0) , Q(1;5) điểm nào cách xa đg thẳng denta nhất?
A. M
B. N
C. P
D. Q
25. Khoảnh cách giữa 2 đg thẳng denta 1: 7x +y -30 và denta 2: 7x +y +120
A. 15
B. 9
C. 9/√50
D. 3√2/2
23. Cho 3 điểm A(0;1) , B(12;5) , C(-3;5) . Đg thẳng nào sau đây cách đều 3 điểm A,B,C
A. -x +y +100
B. x -3y +40
C. 5x -y +10
D. x +y 0
22. Cho 2 điểm A(2;3) , B(1;4) . Đg thẳng nào sau đây cách đều 2 điểm A,B?
A. x -y+1000
B. x -2y...
Đọc tiếp
26. Cho đg thẳng denta 7x +10y -15=0 . Trong các điểm M (1;-3) , N(0;4) , P(8;0) , Q(1;5) điểm nào cách xa đg thẳng denta nhất?
A. M
B. N
C. P
D. Q
25. Khoảnh cách giữa 2 đg thẳng denta 1: 7x +y -3=0 và denta 2: 7x +y +12=0
A. 15
B. 9
C. 9/√50
D. 3√2/2
23. Cho 3 điểm A(0;1) , B(12;5) , C(-3;5) . Đg thẳng nào sau đây cách đều 3 điểm A,B,C
A. -x +y +10=0
B. x -3y +4=0
C. 5x -y +1=0
D. x +y =0
22. Cho 2 điểm A(2;3) , B(1;4) . Đg thẳng nào sau đây cách đều 2 điểm A,B?
A. x -y+100=0
B. x -2y=0
C. x +y -1=0
D. x +2y=0



















