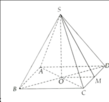
Kim tự tháp thuộc loại hình nghệ thuật nào

Những câu hỏi liên quan
Thành tựu nào sau đây không phải là thành tựu của người Ai Cập cổ đại? A. Chữ tượng hình B. Kim tự tháp
C. Thuật xác ướp D. Bộ luật Ha-mu-ra-bi
Xem thêm câu trả lời
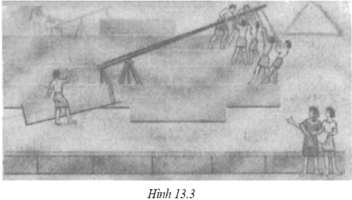
Hình 13.3 mô tả cách những người Ai Cập cổ xây dựng Kim tự tháp. Họ đã sử dụng loại máy đơn giản nào ?
A. mặt phẳng nghiêng
B. ròng rọc
C. đòn bẩy
D. cả ba loại máy kể trên
Chọn C
Quan sát hình vẽ ta thấy những người Ai Cập cổ xây dựng Kim tự tháp đã sử dụng đòn bẩy.
Đúng 0
Bình luận (0)
đồng tháp mười mùa nước nổi sử dụng biện pháp nghệ thuật nào:
Nghệ thuật:
-Ngôi kể thứ nhất
-Sự kiện chân thực,có chọn lọc
Đúng 0
Bình luận (0)
Kim tự tháp là một khối đa diện thuộc hình
A. hình hộp chữ nhật.
B. hình nón cụt.
C. hình lăng trụ đều.
D. hình chóp đều.
Xem thêm câu trả lời
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Đọc tiếp
Kim tự tháp Cheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).
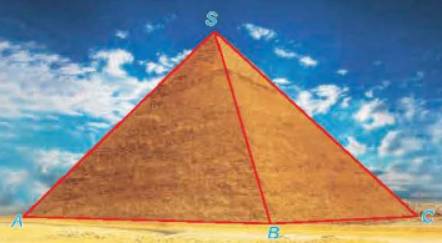
Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Vì AB // CD (ABCD là hình vuông) nên (SC, AB) = (SC, CD)
Xét tam giác SCD có
\(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} = \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCD} \approx 58,{32^0}\)
Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp bằng khoảng 58,320.
Đúng 0
Bình luận (0)
Kim tự tháp Kê-ôp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231m. Tính diện tích xung quanh và thể tích của kim tự tháp
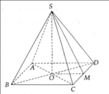
Kim tự tháp có dạng hình chóp tứ giác đều S.ABCD.
Gọi M là trung điểm của cạnh CD; O là tâm của đáy ABCD.
Tính được:
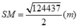
Diện tích xung quanh của kim tự tháp là:
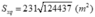
Thể tích của kim tự tháp:
V = 2436819 (m3)
Đúng 0
Bình luận (0)
Để tính cạnh bên và diện tích một mặt bên của kim tự tháp Kê-ốp, chúng ta cần sử dụng các tính chất của hình chóp tứ giác đều.
1. **Tính cạnh bên**:
Trong một hình chóp tứ giác đều, cạnh bên có thể tính được bằng cách sử dụng định lý Pythagoras trên một tam giác vuông có cạnh góc vuông là nửa đường chéo của đáy (đường chéo chia đáy thành hai phần bằng nhau), độ dài một cạnh của đáy và chiều cao của hình chóp.
Trong trường hợp này, nửa đường chéo của đáy là \( \frac{231}{2} = 115.5 \) m, chiều cao của hình chóp là 137 m. Ta sẽ tính độ dài cạnh bên như sau:
\[ \text{Cạnh bên} = \sqrt{{\text{đường chéo}^2 + \text{chiều cao}^2}} \]
\[ \text{Cạnh bên} = \sqrt{{115.5^2 + 137^2}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{13340.25 + 18769}} \]
\[ \text{Cạnh bên} ≈ \sqrt{{32109.25}} \]
\[ \text{Cạnh bên} ≈ 179.25 \, \text{m} \]
2. **Tính diện tích một mặt bên**:
Diện tích một mặt bên của hình chóp tứ giác đều được tính bằng công thức:
\[ \text{Diện tích một mặt bên} = \frac{{\text{cạnh đáy} \times \text{chiều cao}}}{{2}} \]
Trong trường hợp này, cạnh đáy là 231 m và chiều cao là 137 m. Ta sẽ tính diện tích một mặt bên như sau:
\[ \text{Diện tích một mặt bên} = \frac{{231 \times 137}}{{2}} \]
\[ \text{Diện tích một mặt bên} = \frac{{31647}}{{2}} \]
\[ \text{Diện tích một mặt bên} = 15823.5 \, \text{m}^2 \]
Vậy, cạnh bên của kim tự tháp Kê-ốp là khoảng 179.25 m và diện tích của một mặt bên là khoảng 15823.5 \( \text{m}^2 \).
Đúng 0
Bình luận (0)
Kim tự tháp Kê-ốp (Kheops) ở Ai Cập có hình dạng là một hình chóp tứ giác đều. Biết chiều cao kim tự tháp là 137m, cạnh đáy dài 231 m. Tính cạnh bên và diện tích một mặt bên của kim tự tháp.
Hãy cho biết kim tự tháp ở Ai Cập có dạng khối hình học nào?
hình chóp có đáy là hình vuông với bốn mặt bên là tam giác đều.
Đúng 2
Bình luận (0)
Dựa vào SGK trang 13 hình tháp tuổi thành phố HCM năm 1989-1999
Hình dáng tháp tuổi thuộc loại nào?
Nhóm tuổi nào có tỉ lệ lớn nhất?