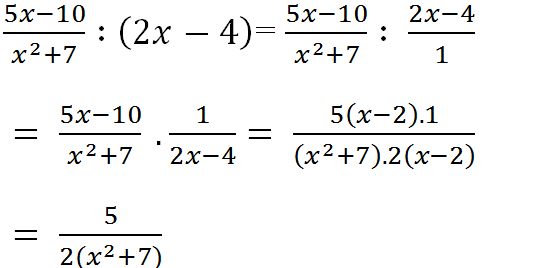Kết quả của phép chia \(\dfrac{x^2+x}{5x^2-10x+5}\) : \(\dfrac{3x+3}{5x-5}\) là :

Những câu hỏi liên quan
làm tính trừ \(\dfrac{5x+y}{xy-5x^2}\)-\(\dfrac{35x^2+8xy+y^2}{xy^225x^3}\)
thực hiện phép tính \(\dfrac{x^3+6x^2-25}{x^3+3x^2-10x}\)-\(\dfrac{x+5}{2x-x^2}\)
b: \(=\dfrac{x^3+6x^2-25}{x\left(x+5\right)\left(x-2\right)}+\dfrac{x+5}{x\left(x-2\right)}\)
\(=\dfrac{x^3+6x^2-25+x^2+10x+25}{x\left(x+5\right)\left(x-2\right)}=\dfrac{x^3+7x^2+10x}{x\left(x+5\right)\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Đúng 1
Bình luận (0)
thực hiện phép tính
\(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{9x^2-4}\)
\(\dfrac{x+25}{2x^2-50}-\dfrac{x+5}{x^2-5x}-\dfrac{5-x}{2x^2+10x}\)
\(\dfrac{1-2x}{2x}-\dfrac{4x}{2x-1}-\dfrac{3}{2x-4x^2}\)
a) \(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{9x^2-4}\)
\(=\dfrac{3x+2-3x+2-3x+6}{\left(3x-2\right)\left(3x+2\right)}\)
\(=\dfrac{-3x+10}{\left(3x-2\right)\left(3x+2\right)}\)
b) \(\dfrac{x+25}{2x^2-50}-\dfrac{x+5}{x^2-5x}-\dfrac{5-x}{2x^2+10x}\)
\(=\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}-\dfrac{x+5}{x\left(x-5\right)}+\dfrac{x-5}{2x\left(x+5\right)}\)
\(=\dfrac{x^2+25x-2\left(x+5\right)^2+\left(x-5\right)^2}{2x\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{x^2+25x-2x^2-20x-50+x^2-10x+25}{2x\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-5x-25}{2x\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{-5\left(x+5\right)}{2x\left(x-5\right)\left(x+5\right)}=\dfrac{-5}{2x\left(x-5\right)}\)
Đúng 0
Bình luận (0)
c) Ta có: \(\dfrac{1-2x}{2x}-\dfrac{4x}{2x-1}-\dfrac{3}{2x-4x^2}\)
\(=\dfrac{-\left(2x-1\right)^2-8x^2+3}{2x\left(2x-1\right)}\)
\(=\dfrac{-\left(4x^2-4x+1\right)-8x^2+3}{2x\left(2x-1\right)}\)
\(=\dfrac{-4x^2+4x-1-8x^2+3}{2x\left(2x-1\right)}\)
\(=\dfrac{-12x^2+4x+2}{2x\left(2x-1\right)}\)
Đúng 0
Bình luận (0)
\(\dfrac{x^2+x}{5x^2+10x+5}:\dfrac{3x+3}{5x-1}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x+1\right)^2}\cdot\dfrac{5x-1}{3\left(x+1\right)}=\dfrac{x\left(5x-1\right)}{15\left(x+1\right)^2}\)
Đúng 1
Bình luận (0)
\(\dfrac{x^2+x}{5x^2+10x+5}:\dfrac{3x+3}{5x-1}=\dfrac{x\left(x+1\right)}{5\left(x^2+2x+1\right)}:\dfrac{3\left(x+1\right)}{5x-1}=\dfrac{x\left(x+1\right)}{5\left(x+1\right)^2}.\dfrac{5x-1}{3\left(x+1\right)}=\dfrac{x\left(5x-1\right)}{15\left(x+1\right)^2}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau :
a) \(\dfrac{5x-10}{x^2+7}:\left(2x-4\right)\)
b) \(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
c) \(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
a.\(\dfrac{5x^3-2x^2+2,5x-2,6}{x^2+3x-2,7}\) tại \(x=\sqrt{0,7}\)
b.\(\dfrac{2x^4-5x^3+2x^2-5x-30}{x^2+10x-15}\) tại \(x=-\sqrt{5}\)
Kết quả của phép chia (2x^4 −10x^3 − x^2 +15x – 3): (2x^2 – 3) là : A. (x^2 – 5x – 1) B. (x^2 + 5x – 1) C. (x^2 – 5x + 1) D. (x^2 + 5x + 1)
thuc hien phep tinh
\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(a.\)
\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}\)
\(=\left(x-5\right)\left(x+5\right).\dfrac{3x-7}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(x+5\right)\left(3x-7\right)}{2\left(x+5\right)}\)
\(=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
\(b.\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x^2-2x+1\right)}.\dfrac{5\left(x-1\right)}{3\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)}{5\left(x-1\right)^2}.\dfrac{5\left(x-1\right)}{3\left(x+1\right)}\)
\(=\dfrac{x\left(x+1\right).5\left(x-1\right)}{5\left(x-1\right)^2.3\left(x+1\right)}\)
\(=\dfrac{x}{3\left(x-1\right)}\)
Đúng 0
Bình luận (0)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}=\dfrac{5x\left(x+1\right)\left(x-1\right)}{15\left(x-1\right)^2\left(x+1\right)}=\dfrac{x}{3\left(x-1\right)}\)\(\left(x^2-25\right):\dfrac{2x+10}{3x-7}=\dfrac{\left(x-5\right)\left(x+5\right)\left(3x-7\right)}{2\left(x+5\right)}=\dfrac{\left(x-5\right)\left(3x-7\right)}{2}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính:
a) \(\dfrac{2x ^2-20x+50}{3x+3}.\dfrac{x^2-1}{4\left(x-5\right)^3}\)
b)\(\dfrac{x^{ }^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
Thực hiện phép tính:
b) \(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(\dfrac{x^2+x}{5x^2-10x+5}:\dfrac{3x+3}{5x-5}\)
\(=\dfrac{x^2+x}{5x^2-10x+5}.\dfrac{5x-5}{3x+3}\)
\(=\dfrac{\left(x^2+x\right)\left(5x-5\right)}{\left(5x^2-10x+5\right)\left(3x+3\right)}\)
\(=\dfrac{x\left(x+1\right)5\left(x-1\right)}{5\left(x^2-2x+1\right)3\left(x+1\right)}\)
\(=\dfrac{5x\left(x+1\right)\left(x-1\right)}{15\left(x-1\right)^2\left(x+1\right)}\)
\(=\dfrac{x}{3\left(x-1\right)}\)
Đúng 0
Bình luận (0)