Muốn một tam thức bậc 2 nhỏ hơn 0 với mọi x thì hệ số a phải nhỏ hơn 0 và Δ < 0 luôn

Cơ mà 1 > 0 rồi nên không có m thoả mãn

Để f(x)<0

`<=>a<0,\Delta<0`

`<=>1<0` vô lý.

Vậy BPT vô nghiệm

\(\Leftrightarrow\left\{{}\begin{matrix}m^2+2>0\left(luôn-đúng\right)\\\Delta'< 0\end{matrix}\right.\) \(\Leftrightarrow\left(m+1\right)^2-\left(m^2+2\right)< 0\Leftrightarrow2m-1< 0\Leftrightarrow m< \dfrac{1}{2}\)

a: \(\Leftrightarrow\left(2m+4\right)^2-4m\cdot9=0\)

\(\Leftrightarrow4m^2+16m+16-36m=0\)

\(\Leftrightarrow m^2-5m+4=0\)

\(\Leftrightarrow\left(m-1\right)\left(m-4\right)=0\)

hay \(m\in\left\{1;4\right\}\)

b: \(\Leftrightarrow\left(2m-8\right)^2-4\left(m^2+m+3\right)=0\)

\(\Leftrightarrow4m^2-32m+64-4m^2-4m-12=0\)

=>-36m+52=0

=>-36m=-52

hay m=13/9

d: \(\Leftrightarrow m^2-4m\left(m+3\right)=0\)

\(\Leftrightarrow m\left(m-4m-12\right)=0\)

=>m(-3m-12)=0

=>m=0 hoặc m=-4

a) PT có nghiệm kép khi △=0

\(\Leftrightarrow\left[2\left(m+2\right)\right]^2-4.m.9=0\)

\(\Leftrightarrow4\left(m^2+4m+4\right)-36m=0\)

\(\Leftrightarrow4m^2-20m+16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=1\end{matrix}\right.\)

Khi đó nghiệm kép của pt là \(x_1=x_2=\dfrac{-2\left(m+2\right)}{2.m}=\dfrac{-2m-4}{2m}=-1-\dfrac{2}{m}\)

+Khi m=4 thì \(x_1=x_2=-1-\dfrac{2}{4}=-\dfrac{3}{2}\)

+Khi m=1 thì \(x_1=x_2=-1-\dfrac{2}{1}=-3\)

a) y′ = 3 x 2  + 2(m + 3)x + m

y′ = 0 ⇔ 3 x 2  + 2(m + 3)x + m = 0

Hàm số đạt cực trị tại x = 1 thì:

y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3

Khi đó,

y′ = 3 x 2  – 3;

y′′ = 6x;

y′′(1) = 6 > 0;

Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.

b) y′ = −( m 2  + 6m) x 2  − 4mx + 3

y′(−1) = − m 2  − 6m + 4m + 3 = (− m 2  − 2m – 1) + 4 = −(m + 1)2 + 4

Hàm số đạt cực trị tại x = -1 thì :

y′(−1) = − ( m + 1 ) 2  + 4 = 0 ⇔ ( m + 1 ) 2  = 4

⇔ 

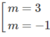
Với m = -3 ta có y’ = 9 x 2  + 12x + 3

⇒ y′′ = 18x + 12

⇒ y′′(−1) = −18 + 12 = −6 < 0

Suy ra hàm số đạt cực đại tại x = -1.

Với m = 1 ta có:

y′ = −7 x 2  − 4x + 3

⇒ y′′ = −14x − 4

⇒ y′′(−1) = 10 > 0

Suy ra hàm số đạt cực tiểu tại x = -1

Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

Đáp án A.

Tập xác định D = R.

y' = x² – 2(m + 1)x + m² – 3, y’’ = 2x – 2(m + 1).

Hàm số đạt cực trị tại x = -1

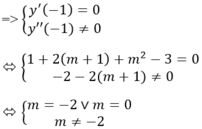
Vậy m = 0 thì hàm số đạt cực trị tại x = -1

Chọn A

Ta có y ' = 3 x 2 + 4 ( m - 1 ) x + m 2 - 4 m + 1 .  Hàm số có hai cực trị

=> y' = 0 có hai nghiệm phân biệt <=> Δ' > 0 <=>  4 ( m - 1 ) 2 - 3 ( m 2 - 4 m + 1 ) > 0

<=>  m 2 + 4 m + 1 > 0

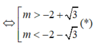
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt  x 1 , x 2  ta có 

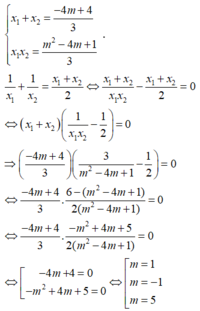
Đối chiếu điều kiện (*) có m = 5 hoặc m = 1