vẽ hình tròn có tâm O
Chứng minh nó méo
Những câu hỏi liên quan
Minh có bài toán muốn nhờ các bạn nó có một hình vuông trong của nó là hình tròn. Đê như sau
Cho hình vuông abc và hình tròn ttâm ở. Chu vi hình tròn tâm o là 28,26. Tính ddidiện tíctích phân tô đâm
Cạnh hình vuông là :
28,26 : 3,14 = 9 (cm)
Diện tích hình tròn là:
(9 : 2) x (9 : 2) x 3,14 = 28,26 (cm2)
Diện tích hình vuông là:
9 x 9 = 81 (cm2)
Diện tích phần tô đậm là:
81 - 28,26 = 52,74 (cm2)
Đáp số: 52,74 cm2
Đúng 0
Bình luận (0)
cho nửa đường tròn (O;R) đường kính ab vẽ tiếp tuyến ax trên cung ab lấy điểm c (c khác a;b) trên tia ax lấy điểm m saon cho ma=mc nối m vói o
chứng minh đường thẳng mc là tiếp tuyến của đường tròn (O;R)
30 tháng 3 2022 lúc 8:44
Nếu ta muốn vẽ một hình tròn mà không có compa thì ta cần làm gì:
A, ta tìm cách để kiếm đc compa
B, mặc kệ cứ vẽ méo là đc
C, tìm mẹo để làm compa
Xem thêm câu trả lời
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm A. 5.38 B. 7.62 C. 5.98 D. 4.44
Đọc tiếp
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
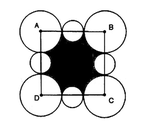
A. 5.38
B. 7.62
C. 5.98
D. 4.44
Cho hình tròn tâm O bán kính 2 cm , A thuộc hình tròn tâm O bán kính 2 cm . Vẽ hình tròn tâm A bán kính 2 cm cắt hình tròn tâm D bán kính 2 cm tại B và C
a ) Chứng minh O thuộc hình tròn tâm A bán kính 2 cm
b ) Chứng minh 3 điểm A , B , C không thẳng hàng
Vẽ một tam giá có ba đường tròn bàng tiếp và một đường tròn nội tiếp.
Chứng minh rằng:Nối ba điểm của một tam giác với trọng tâm của nó thì ta được ba tam giác nhỏ có diện tích bằng nhau.
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau: (1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B. (2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P) (3) Vẽ đường thẳng PC. Em hãy chứng minh đường thẳng PC vuông góc với d. Đố: Tìm thêm một cách dựng nữa (bằng thước và compa...
Đọc tiếp
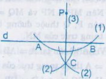
Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
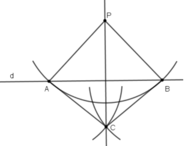
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
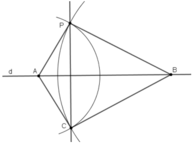
QUẢNG CÁOb) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I đường kính BH, cắt AB ở M. Vẽ đường tròn tâm K có đường kính CH , cắt AC ở Na) Tứ giác AMHN là hình gì ?b) Chứng minh tăng MN là tiếp tuyến chung của hai đường tròn (I) và (K)c) Vẽ tiếp tuyến Ax của đường tròn ngoại tiếp tam giác ABC. CMR Ax//MN
Xem chi tiết
a: Xét (I) có
ΔHMB nội tiếp
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét (K) có
ΔCNH nội tiếp
CH là đường kính
=>ΔCNH vuông tại N
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nên AMHN là hình chữ nhật
b: góc NMI=góc NMH+góc IMH
=góc NAH+góc IHM
=góc CAH+góc HCA=90 độ
=>NM là tiếp tuyến của (I)
góc KNM=góc KNH+góc MNH
=góc KHN+góc MAH
=góc BAH+góc B=90 độ
=>MN là tiếp tuyến của (K)
Đúng 0
Bình luận (0)
Cho \(\widehat {xOy}\). Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong \(\widehat {xOy}\). Nối O với P (Hình 16). Hãy chứng minh rằng , từ đó suy ra OP là tia phân giác của \(\widehat {xOy}\).
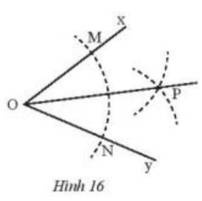
Vì M, N thuộc đường tròn tâm O có cùng bán kính nên OM = ON = bán kính cung tròn tâm O
Từ M, N vẽ 2 cung tròn có cùng bán kính và 2 đường tròn cắt nhau tại P
Suy ra P thuộc cả 2 cung tròn tâm M, N có cùng bán kính nên MP = NP
Xét tam giác OMP và tam giác ONP ta có :
OM = ON
OP cạnh chung
MP = NP
\(\Rightarrow \Delta{OMP}=\Delta{ONP}\) ( c-c-c )
\( \Rightarrow \widehat {MOP} = \widehat {PON}\) (2 góc tương ứng)
Do đó, OP là phân giác \(\widehat {xOy}\)
Đúng 0
Bình luận (0)