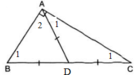
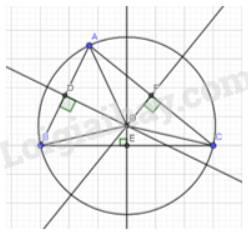
Dùng thước và compa,dựng ba dường trung trực của một tam giác thì vẽ làm sao?

Những câu hỏi liên quan
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
Cách 1:
Gọi trung điểm BC là M
Ta kẻ xy qua M vuông góc với BC
Cách 2:
Từ B, C vẽ 2 cung tròn có bán kính \(R \ge \dfrac{1}{2}BC \)
2 cung tròn giao nhau tại 2 điểm M, N
Kẻ đường thẳng xy đi qua 2 điểm M, N. Ta được đường trung trực xy đi qua chúng
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O bán kính R. Chỉ dùng compa, hãy dựng trực tâm của tam giác ABC.
MN LÀM GIÚP MIK AI ĐÚNG MIK TICK CHO
Chứng minh rằng: Nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại A.
Ứng dụng: Một tờ giấy bị rách mép (h.65). Hãy dùng thước và compa dựng đường vuông góc với cạnh AB tại A.
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
Chỉ dùng thước thẳng và compa, hãy dựng một đa giác đều có 17 cạnh. (chỉ cần nêu bước làm thôi)
Năm 1796, nhà toán học Carl Friedrich Gauss đã tìm được cách vẽ đa giác đều có 17 cạnh bằng thước thẳng và compa, bằng cách xem các đỉnh của đa giác trên vòng tròn như là nghiệm của phương trình số phức zn – 1 = 0.
Năm 1796, nhà toán học Carl Friedrich Gauss đã tìm được cách vẽ đa giác đều có 17 cạnh bằng thước thẳng và compa, bằng cách xem các đỉnh của đa giác trên vòng tròn như là nghiệm của phương trình số phức zn-1=0
a) Dùng thước có chia cm và compa vẽ tam giác ABC cân tại B có cạnh đáy bằng 3cm, cạnh bên bằng 4cm
b) Dùng thước có chia cm và compa vẽ tam giác đều ABC có cạnh bằng 3cm
a) Vẽ đoạn thẳng AC= 3cm.
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 4cm và cung tròn C bán kính 4cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.
b) Tương tự cách vẽ ở câu a với các cung tròn tâm A, tâm C có cùng bán kính 3cm.
Đúng 2
Bình luận (1)
Giải:
a)- Vẽ đoạn thẳng AC= 3cm,
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính4 cm và cung tròn tâm C có bán kính 3cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn AB,BC ta được tam giác ABC.

b) Tương tự cách vẽ ở câu a với cung tròn tâm A, tâm C có cùng bán kính 3 cm
Đúng 1
Bình luận (0)
a) Vẽ đoạn thẳng AC = 3cm.
- Trên cùng một nửa mặt phẳng bờ AC vẽ cung tròn tâm A bán kính 4cm và cung tròn C bán kính 4cm.
- Hai cung tròn trên cắt nhau tại B.
- Vẽ các đoạn thẳng AB, BC ta được tam giác ABC.
b) Tương tự cách vẽ ở câu a với các cung tròn tâm A, tâm C có cùng bán kính 3cm.
Đúng 0
Bình luận (0)
dùng thước và compa , vẽ ba đường trung trực của tam gác . Em có nhận thấy ba đường này cùng đi qua một điểm ko
có
điểm này là tâm đường tròn ngoại tiết của tg
Đúng 0
Bình luận (2)
Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn dfrac{1}{2}AB (Hình 9a)- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
Đọc tiếp
Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn \(\dfrac{1}{2}\)AB (Hình 9a)
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b)
- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN. Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.
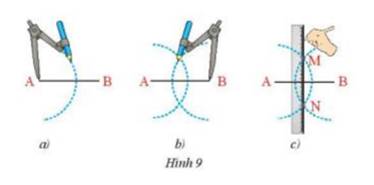
Vì 2 cung tròn cắt nhau tại M nên AM = MB = bán kính cung tròn
Chứng minh tương tự \( \Rightarrow \) AN = BN = bán kính cung tròn
\( \Rightarrow \) Vì M, N cách đều 2 đầu mút của đoạn AB nên M, N thuộc trung trực của AB
Và chỉ có 1 đường thẳng đi qua 2 điểm nên MN là trung trực của AB
Đúng 0
Bình luận (0)
Cho tam giác ABC. Dùng thước và compa vẽ các tia phân giác của các góc A, B, C.
Cách vẽ phân giác của góc A (Dựa trên kết quả bài 20).
Vẽ cung tròn tâm A cung này cắt tia AB ,AC theo thứ tự ở M,N
Vẽ các cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau ở điểm I.
Nối AI, ta được AI là tia phân giác của góc A.
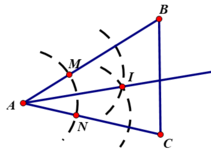
- Tương tự cho cách vẽ tia phân giác của góc B, C
Đúng 0
Bình luận (0)