Cho hình hộp chữ nhật ABCD. A'B'C'D'. Chứng minh :
a)(ABCD)song song với (A'B'C'D')
b)(ABB'A')song song với (CDD'C')
c)(BDC')song song với (AB'D')
Cho hình hộp ABCD. A'B'C'D' Biết ![]() . Khi MN song song với BD’ thì khẳng định nào sau đây đúng
. Khi MN song song với BD’ thì khẳng định nào sau đây đúng
A. k - 1 = - 3 2
B. k + 1 = - 3
C. k + 1 = - 4
D. k + 1 = - 2
Cho hình hộp ABCD. A'B'C'D'. Hai điểm M và N lần lượt nằm trên hai cạnh AD và CC' sao cho \(\dfrac{AM}{MD}=\dfrac{CN}{NC'}\)
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB')
b) Xác định thiết diện của hình hộp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB')
Cho hình thang \(ABCD\) có đáy lớn \(AB\) và \(AB = 2CD\), hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\). Chứng minh rằng \(A'B'C'D'\) cũng là một hình thang và \(A'B' = 2C'D'\).
\(ABCD\) là hình thang có đáy lớn \(AB \Rightarrow AB\parallel CD\).
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của \(ABCD\) là tứ giác \(A'B'C'D'\) nên \(A'B'\parallel C'D'\). Vậy \(A'B'C'D'\) cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà \(AB = 2CD,AB\parallel CD\) và \(A'B'\parallel C'D'\) nên \(A'B' = 2C'D'\).
Cho khối lập phương ABCD A'B'C'D' Người ta dùng 12 mặt phẳng phân biệt (trong đó, 4 mặt song song với (ABCD), 4 mặt song song với (AA'B'B)và 4 mặt song song với (AA'D'D)), chia khối lập phương nhỏ rời nhau và bằng nhau. Biết rằng tổng diện tích tất cả các khối lập phương nhỏ bằng 480. Tính độ dài a của khối lập phương ABCD A'B'C'D'
A. a=2
B. a = 2 3 .
C. a = 2 5 .
D.a=4
Đáp án D
Diện tích toàn phần của hình lập phương cạnh a là S t p = 6 a 2 .
Khi dùng các mặt phẳng như đề bài cho để chia khối lập phương ABCD.A’B’C’D’ ta được 125 khối lập phương nhỏ bằng nhau.
Do đó diện tích toàn phần của 1 khối lập phương nhỏ là 480 125 = 96 25
Gọi cạnh hình lập phương ABCD.A’B’C’D’ bằng a thì độ dài cạnh hình lập phương nhỏ bằng a 5 .
Suy ra diện tích toàn phần của 1 hình lập phương nhỏ là: 6 a 5 2 = 96 25 ⇔ a = 4
Cho hình hộp chữ nhật ABCD.A'BC'D' như hình vẽ.
a) Cặp đường thẳng BB' và A'D'; CD và B'C' có cắt nhau không?
b) Đường thẳng AB có song song với C'D' không? Vì sao?
c) Nêu vị trí tương đối của (ABB'A') với (BDD'B')và (CDD'C')? Giải thích ?
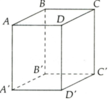
a) BB' và A'D' chéo nhau, CD và B'C' chéo nhau.
b) AB song song với CD (hoặc A'B')
c) (ABB'A') cắt (BDD'B') theo giao tuyến BB', (ABB'A')// (CDD'C') vì AB và AA' song song với (CDD'C').
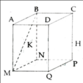
Cho hình hộp A'B'C'D'.ABCD, xác định tiết diện của hình hộp tạo bởi mặt phẳng P đi qua điểm M bất kì nằm trên cạnh BC và mặt phẳng P song song với mặt phẳng ACD'
Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’) song song với mặt phẳng
A. (ABCD)
B. (BCC’B’)
C. (BDA’)
D. (BDC’)
Cho hình thang ABCD (AB song song CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt BC tại E. Chứng minh:
a) Tam giác BDE cân
b) Tam giác ACB = Tam giác BDC
c) ABCD là hình thang cân
Cho hình thang ABCD (AB song song CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt BC tại E. Chứng minh:
a) Tam giác BDE cân
b) Tam giác ACB = Tam giác BDC
c) ABCD là hình thang cân