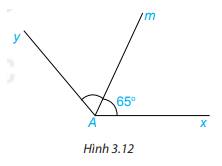
Ta có Am là tia phân giác của góc xAy nên

\(\begin{array}{l}\widehat {xAm} = \frac{1}{2}.\widehat {xAy}\\ \Rightarrow \widehat {xAy} = 2.\widehat {xAm} = 2.65^\circ  = 130^\circ \end{array}\)

Em ơi hình vẽ đâu ?

Chỉ có hai câu h) và i) đúng.

a) sai vì góc 135o > 90o là góc tù.

b) Sai vì góc 75o < 90o là góc nhọn,

c) Sai vì góc có số đo 90o là góc vuông.

d) Sai vì góc có số đo 180o là góc bẹt.

e) Sai vì góc không phải góc tù có thể là một trong các góc: góc nhọn, góc vuông, góc bẹt.

f) Sai vì một góc không phải góc vuông có thể là một trong các góc: góc nhọn, góc tù, góc bẹt.

g) Sai vì mọi góc khác góc bẹt đều bé hơn góc bẹt, không nhất thiết là góc tù.

a: ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(BC^2=6^2+8^2=100\)

=>\(BC=10\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao

nên \(BH\cdot BC=BA^2\)

=>\(BH\cdot10=6^2=36\)

=>BH=36/10=3,6(cm)

XétΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)

nên \(\widehat{C}\simeq37^0\)

b: Xét tứ giác AEHF có

\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)

=>AEHF là hình chữ nhật

=>\(HE^2+HF^2=AH^2\)

Xét ΔHAB vuông tại H có HE là đường cao

nên \(AE\cdot BE=HE^2\)

Xét ΔAHC vuông tại H có HF là đường cao

nên \(AF\cdot FC=HF^2\)

\(AE\cdot BE+AF\cdot FC\)

\(=HE^2+HF^2\)

\(=AH^2\)

c: ΔABC vuông tại A

mà AI là đường trung tuyến

nên AI=BI=CI

IA=IC

=>ΔIAC cân tại I

=>\(\widehat{IAC}=\widehat{ICA}\)

=>\(\widehat{OAF}=\widehat{ACB}\)

AEHF là hình chữ nhật

=>\(\widehat{AFE}=\widehat{AHE}\)

mà \(\widehat{AHE}=\widehat{ABH}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{AFE}=\widehat{ABH}\)

=>\(\widehat{AFO}=\widehat{ABC}\)

\(\widehat{AFO}+\widehat{FAO}=\widehat{ABC}+\widehat{ACB}=90^0\)

=>AO\(\perp\)OF tại O

=>AI\(\perp\)FE tại O

Xét ΔAEF vuông tại A có AO là đường cao

nên \(\dfrac{1}{AO^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

=>ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>góc BAH=góc CAH=50/2=25 độ

c: góc AKC=góc AHC=90 độ

=>AKHC nội tiếp

=>góc KAH=góc KCH

a: Xét ΔDHE vuông tại H và ΔDHF vuông tại H có

DE=DF

DH chung

=>ΔDHE=ΔDHF

b: ΔDHE=ΔDHF

=>góc EDH=góc FDH=40/2=20 độ

c: góc FKD=góc FHD=90 độ

=>FHKD nội tiếp

=>góc KDH=góc KFH

Đáp án là j pn tự biết :)

Mùng 2 Tết r mị chúc pn học giỏi là boy thì đz còn là giri thì xg nha >.<