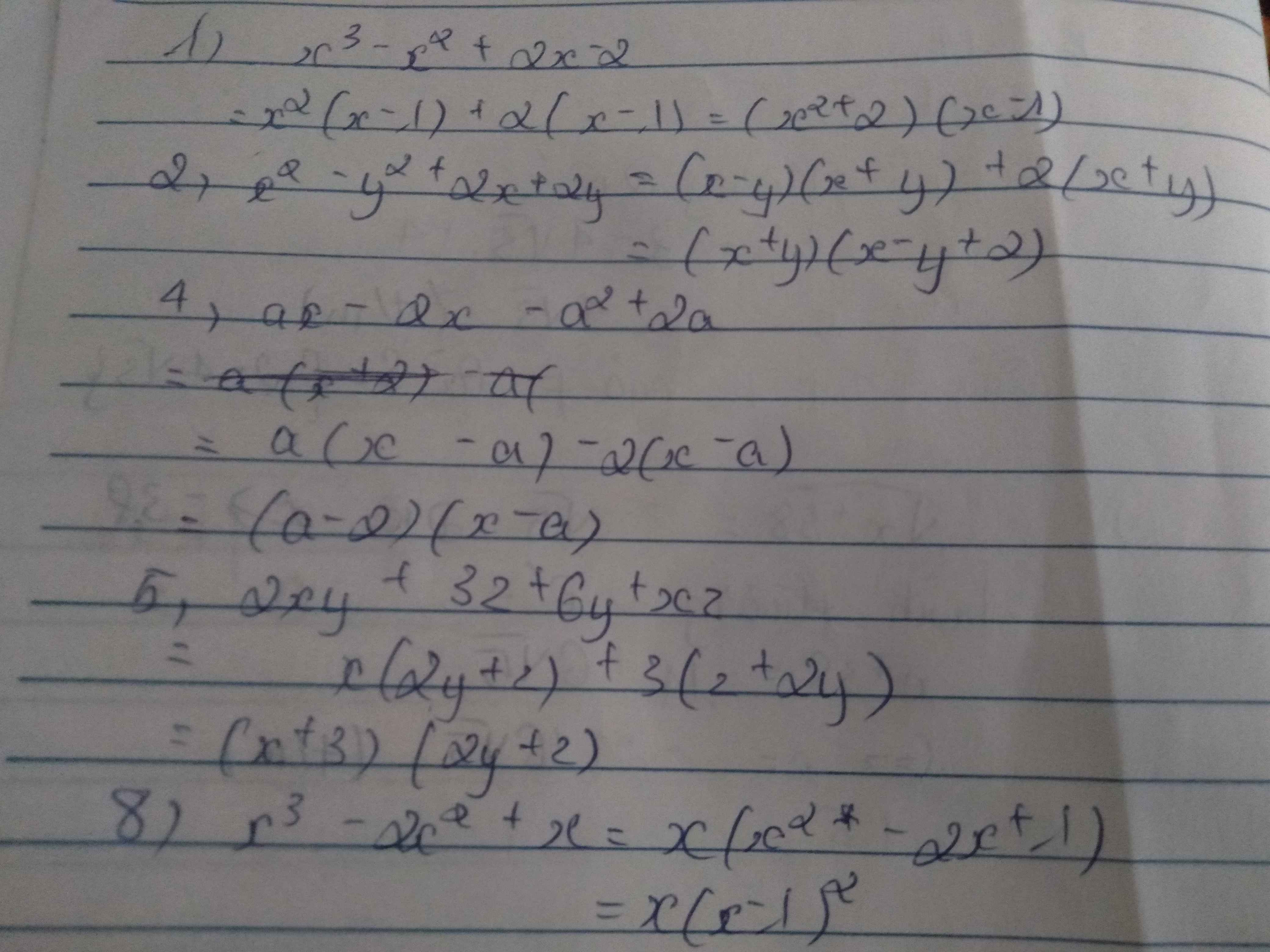(x3-8):(x2+2x+4)

Những câu hỏi liên quan
Thực hiện phép tính: (x3 – 8) : (x – 2)
A. x2 + 2 B. x2 – 2x + 4
C. x2 – 4 D. x3 + 2x + 4
1) x3-x2+2x-2 4) ax-2x-a2+2a 7) x2-6xy-25z2+9y2
2) x2-y2+2x+2y 5) 2xy +3z+6y+xz 8) x3-2x2+x
3) x2/4+2xy+4y2-25 6) x2y2+yz+y3+zx2 9) x4+4
Thực hiện phép tính:
1)(x3-8):(x-2)
2)(x3-1):(x2+x+1)
3)(x3+3x2+3x+1):(x2+2x+1)
4)(25x2-4y2):(5x-2y)
1) \(\left(x^3-8\right):\left(x-2\right)=\left[\left(x-2\right)\left(x^2+2x+4\right)\right]:\left(x-2\right)=x^2+2x+4\)
2) \(\left(x^3-1\right):\left(x^2+x+1\right)=\left[\left(x-1\right)\left(x^2+x+1\right)\right]:\left(x^2+x+1\right)=x-1\)
3) \(\left(x^3+3x^2+3x+1\right):\left(x^2+2x+1\right)=\left(x+1\right)^3:\left(x+1\right)^2=x+1\)
4) \(\left(25x^2-4y^2\right):\left(5x-2y\right)=\left[\left(5x-2y\right)\left(5x+2y\right)\right]:\left(5x-2y\right)=5x+2y\)
Đúng 1
Bình luận (0)
Kết quả phép tính
x
3
+
8
:
x
+
2
là:(A)
x
2
+
4
(B)
x
+
2
2
(C)
x
2
+
2...
Đọc tiếp
Kết quả phép tính x 3 + 8 : x + 2 là:
(A) x 2 + 4
(B) x + 2 2
(C) x 2 + 2 x + 4
(D) x 2 - 2 x + 4
Hãy chọn kết quả đúng.
Đáp án D.
- Cách 1:
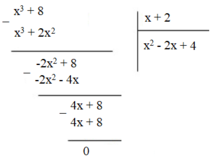
- Cách 2: sử dụng hằng đẳng thức
Ta có:
x 3 + 8 = x 3 + 2 3 x + 2 x 2 - 2 x + 4 ⇒ x 3 + 8 : x + 2 = x 2 - 2 x + 4
⇒ Chọn D
Đúng 0
Bình luận (0)
Kết quả của phép tính (x – 2)(x2 + 2x + 4) là
A. (x + 2)3
B. (x – 2)3
C. x3 + 8
D. x3 – 8
Rút gọn biểu thức.
a)A=(x-3)(x2+3x+9)-(x3+3)
b)B=(2x+1)(4x2-2x+1)-8(x+1/2)(x2-1/2x+1/4)
a) A = (x - 3)(x² + 3x + 9) - (x³ + 3)
= x³ - 3³ - x³ - 3
= (x³ - x³) + (-27 - 3)
= -30
b) B = (2x + 1)(4x² - 2x + 1) - 8(x + 1/2)(x² - 1/2 x + 1/4)
= (2x)³ + 1³ - 8[x³ + (1/2)³]
= 8x³ + 1 - 8(x³ + 1/8)
= 8x³ + 1 - 8x³ - 1
= (8x³ - 8x³) + (1 - 1)
= 0
Đúng 3
Bình luận (1)
1) a) 3xy+2y-4x+8
b) 5xy-3x-11y= -5
c) 4xy+2x+2y=1
2) Tìm các số nguyên x1;x2;x3;...;x7 sao cho (x1)^4+x2)^4+(x3)^+...+(x7)^4=2008
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
Đúng 0
Bình luận (0)
quy đồng các mẫu thức sau
a 1 / x3-8 và 3 / 4-2x
b x / x2-1 và 1 / x2+2x+1
c 1 / x+2 ; x+1 / x2-4x-4 và 5 / 2-x
d 1 / 3x+3y;2x / x2-y2 và x2-xy+y2 / x2-2xy+y2
a) \(\dfrac{1}{x^3-8}=\dfrac{1}{\left(x-2\right)\left(x^2+2x+4\right)}=\dfrac{2}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
\(\dfrac{3}{4-2x}=\dfrac{-3}{2\left(x-2\right)}=\dfrac{-3\left(x^2+2x+4\right)}{2\left(x-2\right)\left(x^2+2x+4\right)}\)
b) \(\dfrac{x}{x^2-1}=\dfrac{x}{\left(x+1\right)\left(x-1\right)}=\dfrac{x\left(x+1\right)}{\left(x+1\right)^2\left(x-1\right)}\)
\(\dfrac{1}{x^2+2x+1}=\dfrac{1}{\left(x+1\right)^2}=\dfrac{x-1}{\left(x+1\right)^2\left(x-1\right)}\)
c) \(\dfrac{1}{x+2}=\dfrac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{1}{x^2-4x+4}=\dfrac{1}{\left(x-2\right)^2}=\dfrac{x+2}{\left(x+2\right)\left(x-2\right)^2}\)
\(\dfrac{5}{2-x}=\dfrac{-5}{x-2}=\dfrac{-5\left(x+2\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)^2}\)
d) \(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{\left(x-y\right)^2}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{2x}{x^2-y^2}=\dfrac{2x}{\left(x+y\right)\left(x-y\right)}=\dfrac{6x\left(x-y\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
\(\dfrac{x^2-xy+y^2}{x^2-2xy+y^2}=\dfrac{x^2-xy+y^2}{\left(x-y\right)^2}=\dfrac{3\left(x^2-xy+y^2\right)\left(x+y\right)}{3\left(x+y\right)\left(x-y\right)^2}=\dfrac{3\left(x^3+y^3\right)}{3\left(x+y\right)\left(x-y\right)^2}\)
Đúng 0
Bình luận (2)
Giải pt : a) 2/-x2+6x-8 - x-1/x-2 = x+3/x-4
b) 2/x3-x2-x+1 = 3/1-x2 - 1/x+1
c) x+2/x-2 - 2/x2-2x = 1/x
d) 5/-x2+5x-6 + x+3/2-x = 0
e) x/2x+2 - 2x/x2-2x-3 = x/6-2x
f) 1/x-1 - 3x2/x3-1 = 2x/x2+x-1