
Những câu hỏi liên quan
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình câu này với
(-154).(-235)+154.(-35)=?
~~~Cảm ơn những người giúp mình câu này trước nka~~~
= 154 . 235 + 154 . (-35)
= 154 . [ 235 + (-35)]
= 154 . 200
= 30800
= 270 nha bạn
Chúc bạn hok tốt
T.I.C.K cho mình nha
Mọi người ơi giúp mình 2 câu này với ạ. Mình cảm ơn mọi người rất nhiều ạ 
Mọi người giúp mình câu này với
a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
b: ΔOCE cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CE tại K
Xét tứ giác OAMK có \(\widehat{OAM}+\widehat{OKM}=90^0+90^0=180^0\)
nên OAMK là tứ giác nội tiếp
=>O,A,M,K cùng thuộc một đường tròn
c: Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AMO}=30^0\)
Xét (O) có
MA,MB là tiếp tuyến
Do đó: MO là phân giác của \(\widehat{AMB}\)
MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}=30^0\cdot2=60^0\)
ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(AM^2=OM^2-OA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(AM=R\sqrt{3}\)
Xét ΔAMB có MA=MB và \(\widehat{AMB}=60^0\)
nên ΔMAB đều
=>\(S_{MAB}=MA^2\cdot\dfrac{\sqrt{3}}{4}=\left(R\sqrt{3}\right)^2\cdot\dfrac{\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)
Đúng 1
Bình luận (0)
Mọi người giúp mình 2 câu này với ạ. Mình làm mãi không được. Cảm ơn mọi người nhiều.
Câu 1:
const fi='dulieu.dat'
fo='thaythe.out'
var f1,f2:text;
a:array[1..100]of string;
n,d,i,vt:integer;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
n:=0;
while not eof(f1) do
begin
n:=n+1;
readln(f1,a[n]);
end;
for i:=1 to n do
begin
d:=length(a[i]);
vt:=pos('anh',a[i]);
while vt<>0 do
begin
delete(a[i],vt,3);
insert('em',a[i],vt);
vt:=pos('anh',a[i]);
end;
end;
for i:=1 to n do
writeln(f2,a[i]);
close(f1);
close(f2);
end.
Đúng 1
Bình luận (0)
Câu 2:
uses crt;
const fi='mang.inp'
fo='sapxep.out'
var f1,f2:text;
a:array[1..100]of integer;
i,n,tam,j:integer;
begin
clrscr;
assign(f1,fi); rewrite(f1);
assign(f2,fo); rewrite(f2);
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
for i:=1 to n do
write(f1,a[i]:4);
for i:=1 to n-1 do
for j:=i+1 to n do
if a[i]>a[j] then
begin
tam:=a[i];
a[i]:=a[j];
a[j]:=tam;
end;
for i:=1 to n do
write(f2,a[i]:4);
close(f1);
close(f2);
end.
Đúng 1
Bình luận (0)
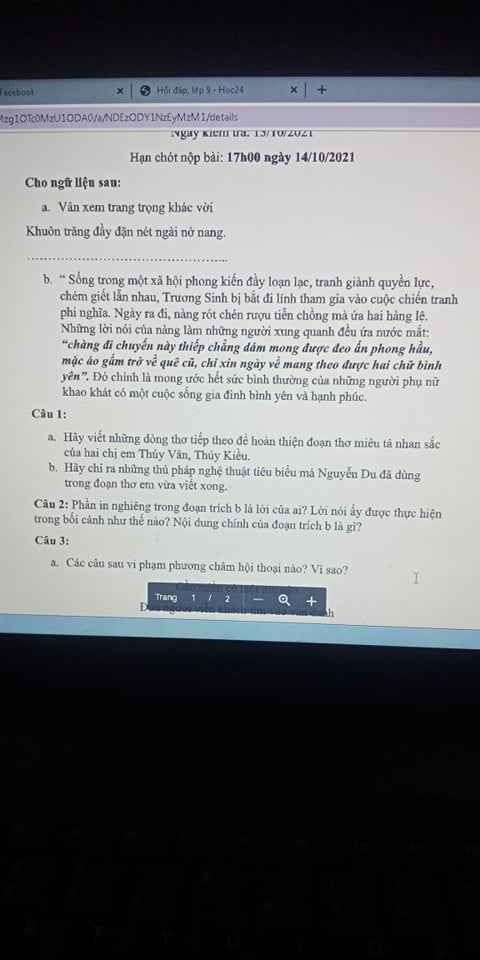 mọi người giúp mình bài này với câu 1 với câu 2 thôi
mọi người giúp mình bài này với câu 1 với câu 2 thôi
mọi người giúp mình câu này với ạ, mình cảm ơn
Đọc tiếp
mọi người giúp mình câu này với ạ, mình cảm ơn
Mọi người ơi giúp mình câu này với mình cảm ơn.

Mọi người ơi giúp mình câu này với mình cảm ơn.

















