cho 2 số u và v biết uv = 9 và u + v = 22 khi đó U và v là hai nghiệm của phương trình

Những câu hỏi liên quan
Tìm hai số x và y với S = x + y ; P = x.y biết :
Nếu có hai số u và v sao cho
u + v = S và uv = P ( S^2 lớn hơn hoặc bằng 4P ) thì u , v là hai nghiệm của phương trình:
x^2 - Sx + P = 0
1. x + y = 3 và xy = 2
*Minh khong ro đề bài có đúng thế này không 1+(2/3)√(x-x2) √x +√(1-x) (DK: 0≤x≤1) Đặt: √x u và √(1-x) v (u;v≥0) Khi đó ta được hệ hai phương trình: {1+(2/3)uvu+v (1) và {u^2+v^21 (2) (1)3(u+v)-2uv3 (2) (u+v)2-2uv1 u+v1 va uv0 .hoac. u+v 2va uv3/2 Dùng định lí Vi-et bạn sẽ tìm được nghiệm (u;v), từ đó tim ra nghiệm x *Nếu đề bai như thế này : 1+[2/(3*√(x-x^2) )] √x +√(1-x)
Đọc tiếp
*Minh khong ro đề bài có đúng thế này không
1+(2/3)√(x-x2) = √x +√(1-x)
(DK: 0≤x≤1)
Đặt: √x = u
và √(1-x) = v (u;v≥0)
Khi đó ta được hệ hai phương trình:
{1+(2/3)uv=u+v (1)
và
{u^2+v^2=1 (2)
(1)<=>3(u+v)-2uv=3
(2)<=> (u+v)2-2uv=1
=> u+v=1 va uv=0 .hoac. u+v= 2va uv=3/2
Dùng định lí Vi-et bạn sẽ tìm được nghiệm (u;v), từ đó tim ra nghiệm x
*Nếu đề bai như thế này :
1+[2/(3*√(x-x^2) )] = √x +√(1-x)
VD: a) u+v= 32 và uv= 231
Ta có u,v là nghiệm của pt
\(x^2-32x+231=0\)
Ta có: Δ'= (-16)2 - 231= 25 >0 ⇒ \(\left\{{}\begin{matrix}x_1=21\\x_2=11\end{matrix}\right.\)
Vậy u= 21 và v= 11 hoặc u=11 và v= 21
b) u+v= -8 và uv= -105
c) u+v= 2 và uv= 9
d) u-v= 5 và uv= 24
b: Phương trình cần tìm là x^2+8x-105=0
=>(x+15)(x-7)=0
=>x=-15 hoặc x=7
c: Phương trình có hai nghiệm u,v thỏa mãn là x^2-2x+9=0
=>PTVN
d: Phương trình có hai nghiệm u,v thỏa mãn là x^2-5x+24=0
=>PTVN
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v = 32 , uv = 231
b) u + v = -8, uv = -105
c) u + v = 2, uv = 9
a) S = 32 ; P = 231 ⇒ S 2 – 4 P = 322 – 4 . 231 = 100 > 0
⇒ Tồn tại u và v là hai nghiệm của phương trình: x 2 – 32 x + 231 = 0 .
Ta có: Δ = ( - 32 ) 2 – 4 . 231 = 100 > 0
⇒ PT có hai nghiệm:
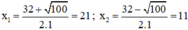
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) S = -8; P = -105 ⇒ S 2 – 4 P = ( - 8 ) 2 – 4 . ( - 105 ) = 484 > 0
⇒ u và v là hai nghiệm của phương trình: x 2 + 8 x – 105 = 0
Ta có: Δ ’ = 4 2 – 1 . ( - 105 ) = 121 > 0
Phương trình có hai nghiệm:
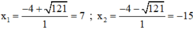
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) S = 2 ; P = 9 ⇒ S 2 – 4 P = 2 2 – 4 . 9 = - 32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Đúng 0
Bình luận (0)
Tìm hai số u và v biết: u +v =1, uv =- 42 và u >v .
\(u+v=1\Rightarrow v=1-u\)
Thế vào \(uv=-42\Rightarrow u\left(1-u\right)=-42\)
\(\Rightarrow u^2-u-42=0\Rightarrow\left[{}\begin{matrix}u=7\Rightarrow v=-6\\u=-6\Rightarrow v=7>u\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
u + v = 2, uv = 9
S = 2 ; P = 9 ⇒ S2 – 4P = 22 – 4.9 = -32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v =32; uv = 231; b) u + v = -8; uv = -105;
c) u + v = 2; uv = 9.
a) u và v là nghiệm của phương trình: x2 – 32x + 231 = 0
∆’ = 162 – 231 = 256 – 231 = 25, \(\sqrt{\text{∆}'}\) = 5 . x1 = 21, x2 = 11
Vậy u = 21, v = 11 hoặc u = 11, v = 21
b) u, v là nghiệm của phương trình:
x2 + 8x – 105 = 0, ∆’ = 16 + 105 = 121, \(\sqrt{\text{∆}'}\) = 11 . x = -4 + 11 = 7
x2 = -4 – 11 = -15
Vậy u = 7, v = -15 hoặc u = -15, v = 7
c) Vì 22 – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.
Đúng 0
Bình luận (0)
a) u và v là nghiệm của phương trình: x2 – 32x + 231 = 0
∆’ = 162 – 231 = 256 – 231 = 25, √∆' = 5 . x1 = 21, x2 = 11
Vậy u = 21, v = 11 hoặc u = 11, v = 21
b) u, v là nghiệm của phương trình:
x2 + 8x – 105 = 0, ∆’ = 16 + 105 = 121, √∆' = 11 . x = -4 + 11 = 7
x2 = -4 – 11 = -15
Vậy u = 7, v = -15 hoặc u = -15, v = 7
c) Vì 22 – 4 . 9 < 0 nên không có giá trị nào của u và v thỏa mãn điều kiện đã cho.
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v = 12, uv = 28 và u > v
b) u + v = 3, uv = 6
a) S = 12, P = 28 ⇒ S 2 – 4 P = 32 > 0
⇒ u, v là hai nghiệm của phương trình: x 2 – 12 x + 28 = 0 .
Có a = 1; b = -12; c = 28 ⇒ Δ ’ = ( - 6 ) 2 – 28 = 8 > 0
Phương trình có hai nghiệm x 1 = 6 + 2 √ 2 ; x 2 = 6 - 2 √ 2
Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2
b) S = 3; P = 6 ⇒ S 2 – 4 P = - 15 < 0
Vậy không tồn tại u, v thỏa mãn yêu cầu.
Đúng 0
Bình luận (0)
Tìm 2 số u và v trong mỗi trường hợp sau:
a, u+v=32, uv=231, b,u+v=-8, uv=-105, c, u+v=2, uv=9
Tức là như thế này:
a/ \(u+v=32\Rightarrow u=32-v\)hoặc \(v=32-u\)(Cái này tùy bạn chọn nhưng mình chọn cái 1)
Ta có: \(uv=231\)
\(\Leftrightarrow\left(32-v\right)v=231\)
\(\Leftrightarrow32v-v^2-231=0\)
\(\Leftrightarrow-v^2+32v-231=0\)
Sau đó bạn giải \(\Delta\)tìm được \(v\)và có \(v\)rồi thì ra cái còn lại.
Các câu sau tương tự không có gì hết
Đúng 0
Bình luận (0)
a) từ tổng u+v=32 => u=32-v rồi thay u=32-v vào uv=231 sẽ tìm ra u;v
các câu sau làm tương tự
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


















