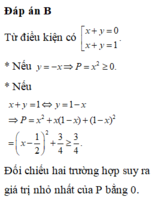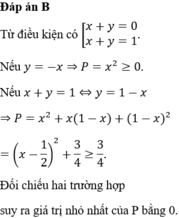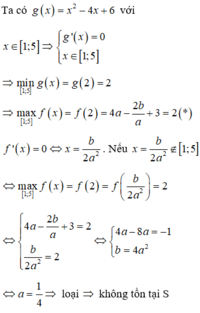Giá trị nhỏ nhất của x thoả mãn x2+5x+10. (Giúp với)

Những câu hỏi liên quan
1,Trung bình cộng các giá trị x thoả mãn 4(x-1)^2=x^2
2,Giá trị nhỏ nhất của x^2-2x-3
3,Tổng các giá trị x thoả mãn x^2-5x+4
Bài 1 : \(4\left(x-1\right)^2=x^2\Leftrightarrow4\left(x^2-2x+1\right)=x^2\)
\(\Leftrightarrow4x^2-8x+4-x^2=0\Leftrightarrow3x^2-8x+4=0\)
\(\Leftrightarrow\left(3x-2\right)\left(x-2\right)=0\Leftrightarrow x=\frac{2}{3};2\)
Áp dụng với trung bình cộng 2 số : \(\frac{\frac{2}{3}+2}{2}=\frac{8}{\frac{3}{2}}=\frac{4}{3}\)
Bài 2 : Đặt A = \(x^2-2x-3=x^2-2x+1-4=\left(x-1\right)^2-4\ge-4\)
Dấu ''='' xảy ra <=> x = 1
Vậy GTNN A là -4 <=> x = 1
Bài 3 : \(x^2-5x+4=x^2-4x-x+4=x\left(x-4\right)-\left(x-4\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-4\right)\Leftrightarrow x=1;4\)
Tổng các giá trị x là : \(1+4=5\)
3, Tổng các giá trị của x thỏa mãn:
\(x^2-5x+4=0\)
\(\Leftrightarrow x^2-4x-x+4=0\)
\(\Leftrightarrow x\left(x-4\right)-\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=1\end{cases}}\)
Vậy tổng các giá trị x thỏa mãn phương trình: S = 4 + 1 = 5
Cho phương trình x2 + (m+1)x + 2 = 0.
Tìm giá trị của m để hai nghiệm x1, x2 của phương trình thoả mãn x12 + x22 nhỏ nhất.
\(\Delta=\left(m+1\right)^2-4.1.2=\left(m+1\right)^2-8\)
Để PT có 2 nghiệm thì:
\(\Delta\ge0\Leftrightarrow\left(m+1\right)^2-8\ge0\\ \Leftrightarrow\left(m+1\right)^2\ge8\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=-\left(m+1\right)\\x_1x_2=2\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1^2+2x_1x_2+x_2^2-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2.2=\left(m+1\right)^2-4\)
Mà \(\left(m+1\right)^2\ge8\) nên \(\left(m+1\right)^2-4\ge4\)
\(\Rightarrow min_{x_1^2+x_2^2}=4\) (dấu bằng xảy ra)
\(\Leftrightarrow\left(m+1\right)^2=8\)
\(\Leftrightarrow m^2+2m+1=8\\\Leftrightarrow m^2+2m-7=0 \)
\(\Leftrightarrow m=-1\pm2\sqrt{2}\)
Đúng 3
Bình luận (0)
cho hai số thực x>0,y>0 thoả mãn xy=6.Tìm giá trị nhỏ nhất của biểu thức P=x2+y2
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
Đúng 1
Bình luận (0)
Cho các số nguyên x,y thoả mãn 5x - 2y = 1. Tìm giá trị nhỏ nhất của biểu thức T = 3 | x | + 5 | y |
Giải thích đầy đủ nha mn giúp mình mai thi HKII rùi
Cho các số thực x,y thoả mãn x+y 2.Tìm giá trị nhỏ nhất của biểu thức: A x3�3 + y3�3 + x2�2 + y2
Đọc tiếp
Cho các số thực x,y thoả mãn x+y =2.Tìm giá trị nhỏ nhất của biểu thức: A= + + +
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
Đúng 0
Bình luận (0)
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P = x 2 + x y + y 2 bằng
A. 3 4
B. 0
C. 1 4
D. 1 2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức P
x
2
+
x
y...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P= x 2 + x y + y 2 bằng
A. 3 4
B. 0.
C. 1 4
D. 1 2
Cho phương trình m2 x+6(x +1 ) =m(5x + 3) (m là tham số) (1). Tìm m để phương trình (1) có một nghiệm duy nhất thỏa mãn biểu thức A= x2 + 2x + 3/x2 + 2 đạt giá trị nhỏ nhất
giúp e với ạ mai thi rồi cảm ơn !!!
Xét các hàm số
f
x
a
x
2
−
b
a
x
+
3
và
g
x
x
2
−
4
x
+
6
trên đoạn [1;5]. Biết trên đoạn [1;5] thì giá trị lớn nhất của f(x) bằng giá trị nhỏ nhất của g(x) và đạt tại cùng một điểm . Tính S là tổng các giá trị a, b thoả mãn...
Đọc tiếp
Xét các hàm số f x = a x 2 − b a x + 3 và g x = x 2 − 4 x + 6 trên đoạn [1;5]. Biết trên đoạn [1;5] thì giá trị lớn nhất của f(x) bằng giá trị nhỏ nhất của g(x) và đạt tại cùng một điểm . Tính S là tổng các giá trị a, b thoả mãn yêu cầu bài toán .
A. S = 0
B. S = -1
C. S = 1 2
D. không tồn tại S