Gọi 2 điểm cố định là \(A\left(x_0;y_0\right)\)

Thay vào ptđt (d) ta được : \(y_0=mx_0+m+1\Leftrightarrow mx_0+m+1-y_0=0\)

\(\Leftrightarrow m\left(x_0+1\right)+\left(1-y_0\right)=0\)

Đẳng thức xảy ra khi \(\hept{\begin{cases}x_0+1=0\\1-y_0=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\Rightarrow A\left(-1;1\right)\)

Vậy d luôn đi qua 1 điểm cố định A(-1;1) 

Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình :

14.x2=x−114.x2=x−1

<=> x² = 4x - 4

<=> x² - 4x + 4 = 0 <=> (x - 2)² = 0 <=> x - 2= 0 <=> x = 2

=> y = 2-1 = 1

Vậy (P) cắt (d) tại 1 điểm duy nhất là (2;1) 

=> đpcm 

đúng ko ????????????? 

sai thì cho mik xin lỗi

Giả sử ( x 0 ; y 0  ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.

Ta có:

m x 0  + 3 + (3m - 1)  y 0  = 0 với mọi m

⇔ m x 0  + 3 + 3m y 0  - y 0  = 0 với mọi m

⇔ m( x 0  + 3 y 0 ) + 3 - y 0 = 0 với mọi m

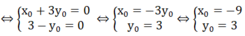
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)

 Gọi \(M\left(x_o;y_o\right)\) là điểm cố định mà đường thẳng \(\left(dm\right):y=mx-2m+1\) luôn đi qua 

\(\Leftrightarrow y_o=mx_o+2m+1\)

\(\Leftrightarrow m\left(x_o+2\right)+1-y_o=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_o+2=0\\1-y_o=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_o=-2\\y_o=1\end{matrix}\right.\)

\(\Leftrightarrow M\left(-2;1\right)\) là điểm cố định mà đường thẳng \(\left(dm\right)\) luôn đi qua \(\left(đpcm\right)\)

Gọi A(x_o;y_o) là điểm cố định mà đths trên luôn đi qua với ∀m

Do đó pt sau luôn đúng với∀m

 y_o=mx_o-2m-4

⇔y_o+4 = mx_o-2m

Vì pt trên đúng với ∀ m nên: y_o+4=0⇔y_o=-4

                                              x_o-2=0⇔x_o=2

Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà \(\left(d\right)\) luôn đi qua

\(\Leftrightarrow y_0=\left(1+m\right)x_0-2m+4=x_0+mx_0-2m+4\\ \Leftrightarrow m\left(x_0-2\right)+\left(x_0-y_0+4\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=2\\2-y_0+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=6\end{matrix}\right.\)

Vậy \(\left(d\right)\) luôn đi qua \(A\left(2;6\right)\) cố định với mọi m

y=mx+2x-m+3=m(x-1)+2x+3

ĐIểm mà d luôn đi qua là:

x-1=0 và y=2x+3

=>x=1 và y=2+3=5

y=m(x-2)+1

=>m(x-2)-y+1=0

Điểm mà (d) luôn đi qua có tọa độ là:

x-2=0 và 1-y=0

=>x=2 và y=1

Ta có: (d1): y=mx-y=2

\(\Leftrightarrow y=mx-2\)

\(\Leftrightarrow y+2=mx\)

Tọa độ điểm B cố định là nghiệm của hệ phương trình:

\(\left\{{}\begin{matrix}y+2=0\\x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\x=0\end{matrix}\right.\)

Vậy: (d1) luôn đi qua B(0;-2)

Ta có: (d2): (2-m)x+y=m

\(\Leftrightarrow y=mx-2x+m\)

\(\Leftrightarrow y+2x=m\left(x+1\right)\)

Tọa độ điểm C cố định là nghiệm của hệ phương trình:

\(\left\{{}\begin{matrix}x+1=0\\y+2x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2x=-2\cdot\left(-1\right)=2\end{matrix}\right.\)

Vậy: (d2) luôn đi qua điểm C(-1;2)

Gọi \(B\left(x_B;y_B\right)\) là điểm cố định mà \(\left(d_1\right)\) đi qua

\(\Rightarrow mx_B-y_B=2\Rightarrow mx_B-\left(y_B+2\right)=0\Rightarrow\left\{{}\begin{matrix}x_B=0\\y_B=-2\end{matrix}\right.\)

\(\Rightarrow B\left(0;-2\right)\Rightarrow\left(d_1\right)\) luôn đi qua điểm \(B\left(0;-2\right)\) cố định 

Gọi \(C\left(x_C;y_C\right)\) là điểm cố định mà \(\left(d_2\right)\) đi qua

\(\Rightarrow\left(2-m\right)x_C+y_C=m\Rightarrow2x_C-mx_C-m+y_C=0\)

\(\Rightarrow-m\left(x_C+1\right)+2x_C+y_C=0\Rightarrow\left\{{}\begin{matrix}x_C=-1\\2x_C+y_X=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x_C=-1\\y_C=2\end{matrix}\right.\)

\(\Rightarrow C\left(-1;2\right)\Rightarrow\left(d_2\right)\) luôn đi qua điểm \(C\left(-1;2\right)\) cố định

Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đường thẳng đã cho đi qua

\(\Rightarrow\) Với mọi m ta luôn có:

\(\left(2m^2+m+4\right)x_0-\left(m^2-m-1\right)y_0-5m^2-4m-13=0\)

\(\Leftrightarrow\left(2x_0-y_0-5\right)m^2+\left(x_0+y_0-4\right)m+4x_0+y_0-13=0\)

\(\Rightarrow\left\{{}\begin{matrix}2x_0-y_0-5=0\\x_0+y_0-4=0\\4x_0+y_0-13=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_0=3\\y_0=1\end{matrix}\right.\)

Vậy khi m thay đổi thì đường thẳng luôn đi qua điểm cố định có tọa độ \(\left(3;1\right)\)