Giúp mk câu 4 ạ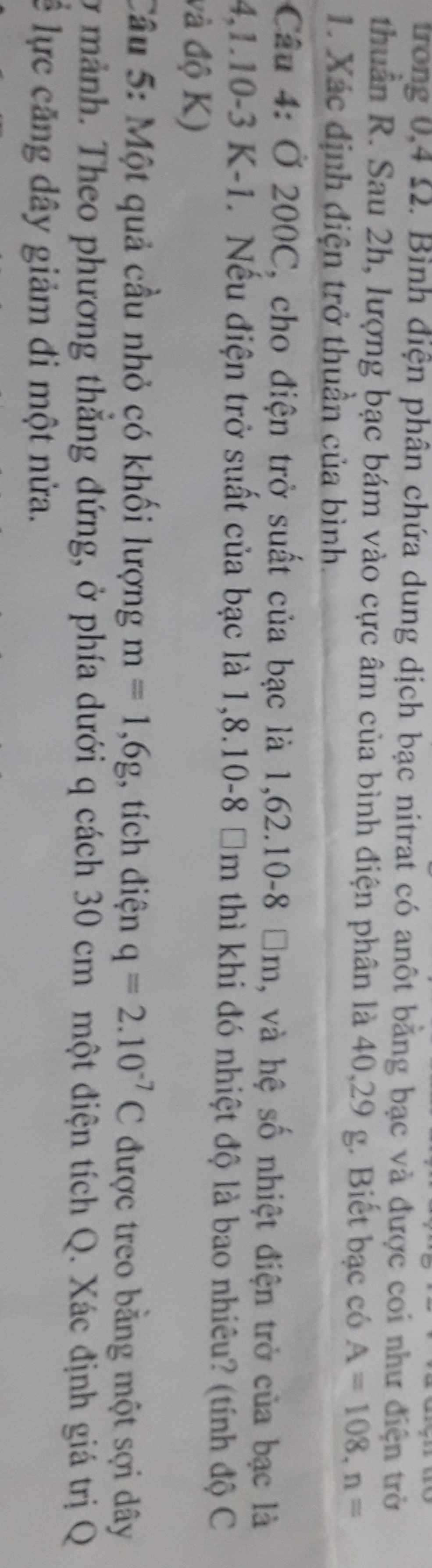

Những câu hỏi liên quan
Giúp mk câu 3 và câu 4 với ạ , mk cần gấp lắm ạ 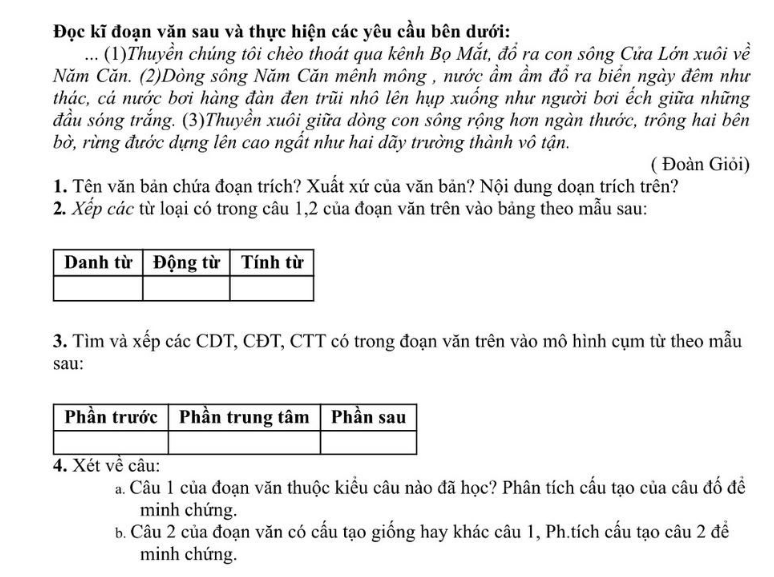
ddđlàm giúp mk câu 4 mk cần gấp ạ hộ mk vscảm ơn nhìu
Đọc tiếp
ddđlàm giúp mk câu 4 mk cần gấp ạ ![]()
| hộ mk vs |
| cảm ơn nhìu |
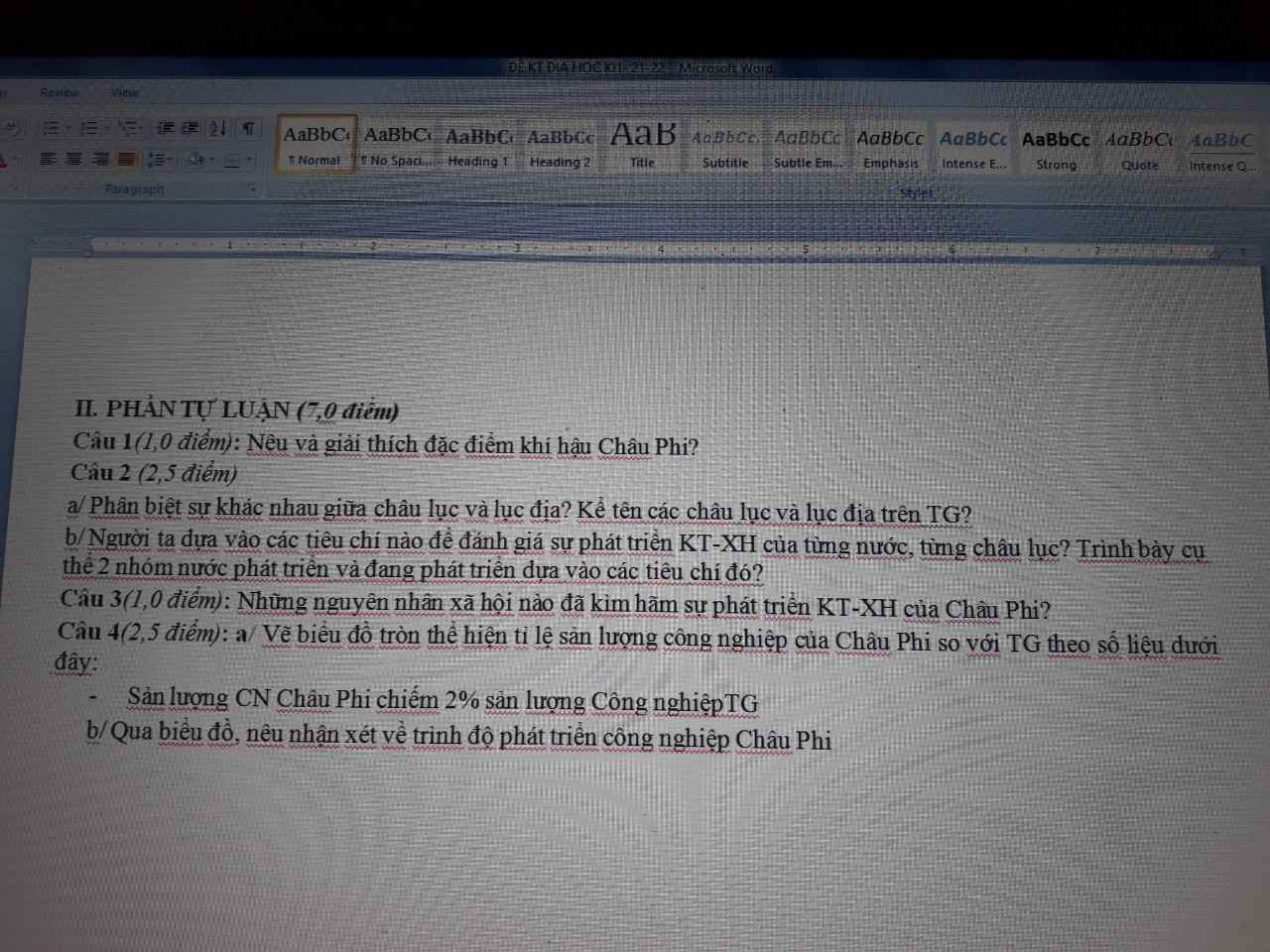
Giải giúp mk 2 bài này với ạ mk đag cần gấp . dịch giúp mk 4 câu của part 7
P6:
1. big
2. been
3. bought
4. people
P7:
1. T
2. F
3. F
4. F
Đúng 1
Bình luận (1)
Giúp mk câu 4 vs ạ
Câu 4:
a) Xét tứ giác AIMK có
\(\widehat{AIM}+\widehat{AKM}=180^0\)
nên AIMK là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Giúp mk câu 4 với ạ
4 Bac Giang city is reported to have increasingly developed in the past few years
Đúng 0
Bình luận (0)

giúp mk giải chi tiết 4 câu trên ạ
mk cảm ơn
\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)
\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)
Đúng 0
Bình luận (0)
\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)
(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")
\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)
\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)
\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)
\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)
\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)
\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)
\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)
Đúng 0
Bình luận (0)
\(7;\) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}< 2x+\dfrac{1}{2x}-1\left(đk:x>0\right)\)
\(\Leftrightarrow3\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< 2\left(x+\dfrac{1}{4x}\right)-1\left(1\right)\)
\(đặt:\sqrt{x}+\dfrac{1}{2\sqrt{x}}=t>0\)
\(\Leftrightarrow t^2=\sqrt{x}^2+2.\sqrt{x}.\dfrac{1}{2\sqrt{x}}+\left(\dfrac{1}{2\sqrt{x}}\right)^2=x+\dfrac{1}{4x}+1\)
\(\Rightarrow x+\dfrac{1}{4x}=t^2-1\)
\(\left(1\right)\Leftrightarrow3t< 2\left(t^2-1\right)-1\)
\(\Leftrightarrow2t^2-3t-3>0\Leftrightarrow\left[{}\begin{matrix}t< \dfrac{3-\sqrt{33}}{4}\\t>\dfrac{3+\sqrt{33}}{4}\end{matrix}\right.\)
\(\Rightarrow\sqrt{x}+\dfrac{1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\dfrac{2x+1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)
\(\Leftrightarrow\sqrt{x}< \dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(2x+1\right)\ge0\\x< \left[\dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\right]^2\\\end{matrix}\right.\)
đến đây dễ dàng rồi như mấy ý trên bạn tự giải quyết để tìm ra x
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp mk vài 4 vs ạ mk chỉ cần câu a thôi
4:
a: Xét ΔADH vuông tại D và ΔHEA vuông tại E có
AH chung
góc HAD=góc AHE
=>ΔADH=ΔHEA
=>DH=EA
b: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
mà AH cắt DE tại I
nên IA=IH=ID=IE
c: ADHE là hình chữ nhật
=>góc ADE=góc AHE
mà góc AHE=góc ACB
nên góc ADE=góc ACB
Đúng 0
Bình luận (0)
Mn giải giúp mk câu 4 ạ
Câu 4:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Vậy: BC=10cm
Đúng 1
Bình luận (0)
a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(gt)
nên \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)(Tính chất tia phân giác của tam giác)
hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
b) Xét ΔABD vuông tại A và ΔEBC vuông tại E có
\(\widehat{ABD}=\widehat{EBC}\)(BD là tia phân giác của \(\widehat{ABC}\))
Do đó: ΔABD\(\sim\)ΔEBC(g-g)
Đúng 1
Bình luận (0)

giúp mk câu 4 với ạ! thanks

















