Kẻ DH ⊥ BC.

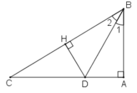
Xét hai tam giác vuông ABD và HBD, ta có:

∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).

Cạnh huyền BD chung

∠BAD = ∠BHD = 90º

Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)

⇒ AD = HD (2 cạnh tương ứng) (1)

Trong tam giác vuông DHC có ∠DHC = 90o

⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)

Từ (1) và (2) suy ra: AD < DC

Kẻ DE⊥ BC

Xét △ABC và △BDE có: Â=Ê=90*

∠ABD=∠DBE (BD phân giác ∠B)

BD: cạnh chung

⇒ △ABC = △BDE ( cạnh huyền-góc nhọn)

⇒ AD=DE ( 2 cạnh tương ứng)

Xét △EDC có: Ê=90*

⇒ Ê>∠C (theo nhận xét)

⇒ DC>DE (theo quan hệ góc,cạnh đối diện trong tam giác)

mà AD=DE ⇒DC>AD (đpcm)

Chọn B

Xét hai tam giác vuông DBA và DHB có:

BD là cạnh chung

\(\widehat{ABD}=\widehat{DHB}\)( BD là tia phân giác )

\(\Rightarrow\Delta DBA=\Delta DBH\left(ch-gn\right)\)

\(\Rightarrow AB=DH\)( 2 cạnh bằng nhau )

Tam giác vuông DHC có: 

DC là canh huyền suy ra DC là cạnh lớn nhất

\(\Rightarrow DC>DH\)

Mà DH = AD nên AD < DC

*Đảm bảo đúng 100% nhé!! 😊*

Giải:

Dựng DH vuông góc BC (H thuộc BC)

Xét hai tam giác vuông ABD và HBD có:

Góc A = Góc H (=90°)

BD: cạnh chung

Góc ABD = Góc HBD

=> Tam giác ABD = Tam giác HBD (cạnh huyền- góc nhọn)

=> AD = DH (2 cạnh tương ứng)

Xét tam giác vuông DHC vuông tại H có DC là cạnh huyền => DC là cạnh lớn nhất trong tam giác DHC

Do đó: AD = DH > DC (đpcm)

Câu B:

Xét hai tam giác vuông ABD và HBD, ta có:

∠B1 = ∠B2 ( vì BD là tia phân giác của góc ABC).

Cạnh huyền BD chung

∠BAD = ∠BHD = 90º

Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)

⇒ AD = HD (2 cạnh tương ứng) (1)

Trong tam giác vuông DHC có ∠DHC = 90o

⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)

Từ (1) và (2) suy ra: AD < DC

cảm ơn nhma có thể vẽ hình đc k câu a nx ạ

Câu a:

Vì góc ADC là góc ngoài tại đỉnh D của tam giác BDC nên

\(\widehat{ADB}=\widehat{DBC}+\widehat{C}\)

Suy ra   \(\widehat{ADB}>\widehat{DBC}\)

Mà  \(\widehat{DBC}=\widehat{DBA}\)  (vì BD là tia phân giác của góc ABC)

Do đó  \(\widehat{ADB}>\widehat{DBA}\) ➩ AB > AD  (cạnh đối diện với góc lớn hơn thì lớn hơn).

P/s: Khong biết đúng ko 

a: Xét ΔBAD vuông tai A và ΔBHD vuông tại H có

BD chung

góc ABD=góc HBD

Do đó: ΔBAD=ΔBHD

Suy ra: AD=HD

b: ta có: AD=HD

mà HD<DC

nen AD<DC

c: Xét ΔBHK vuông tại H và ΔBAC vuông tạiA có

BH=BA

góc HBK chung

Do đó:ΔBHK=ΔBAC
Suy ra BK=BC

hay ΔBKC cân tại B

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có

BD chung

góc ABD=góc HBD

=>ΔBAD=ΔBHD

=>DA=DH

b: DA=DH

DH<DC

=>DA<DC

c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có

BH=BA

góc HBK chung

=>ΔBHK=ΔBAC

=>BK=BC

=>ΔBKC cân tại B

https://hoidapvietjack.com/q/804157/cho-tam-giac-abc-vuong-tai-a-tia-phan-giac-cuaabc-cat-ac-tai-d-tu-d-ke-dh-vuong-

Không đủ dữ kiện để so sánh. Bạn xem có viết thiếu điều kiện gì không>