Cho x,y thuộc \(Z^+\) x+y=2003 Tìm GTLN và GTNN của \(P=x\left(x^2+y\right)+y\left(y^2+x\right)\)

Những câu hỏi liên quan
cho x,y,z dương thỏa mãn \(5\left(x+y+z\right)^2\ge14\left(x^2+y^2+z^2\right)\). tìm GTNN và GTLN của \(P=\dfrac{2x+z}{x+2z}\)
Đúng 0
Bình luận (0)
a,Cho x,y,z tm \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\x+y+z=4\end{matrix}\right.\). CM: \(-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b, cho \(x^2+3y^2=1\). Tìm GTLN, GTNN của\(P=x-y\)
c, Cho \(P=\dfrac{x^2-\left(x-4y\right)^2}{x^2+4y^2}\left(x^2+y^2>0\right)\)
Tìm GTLN của P
\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Đúng 3
Bình luận (2)
Bài a hình như sai đề rồi bạn.
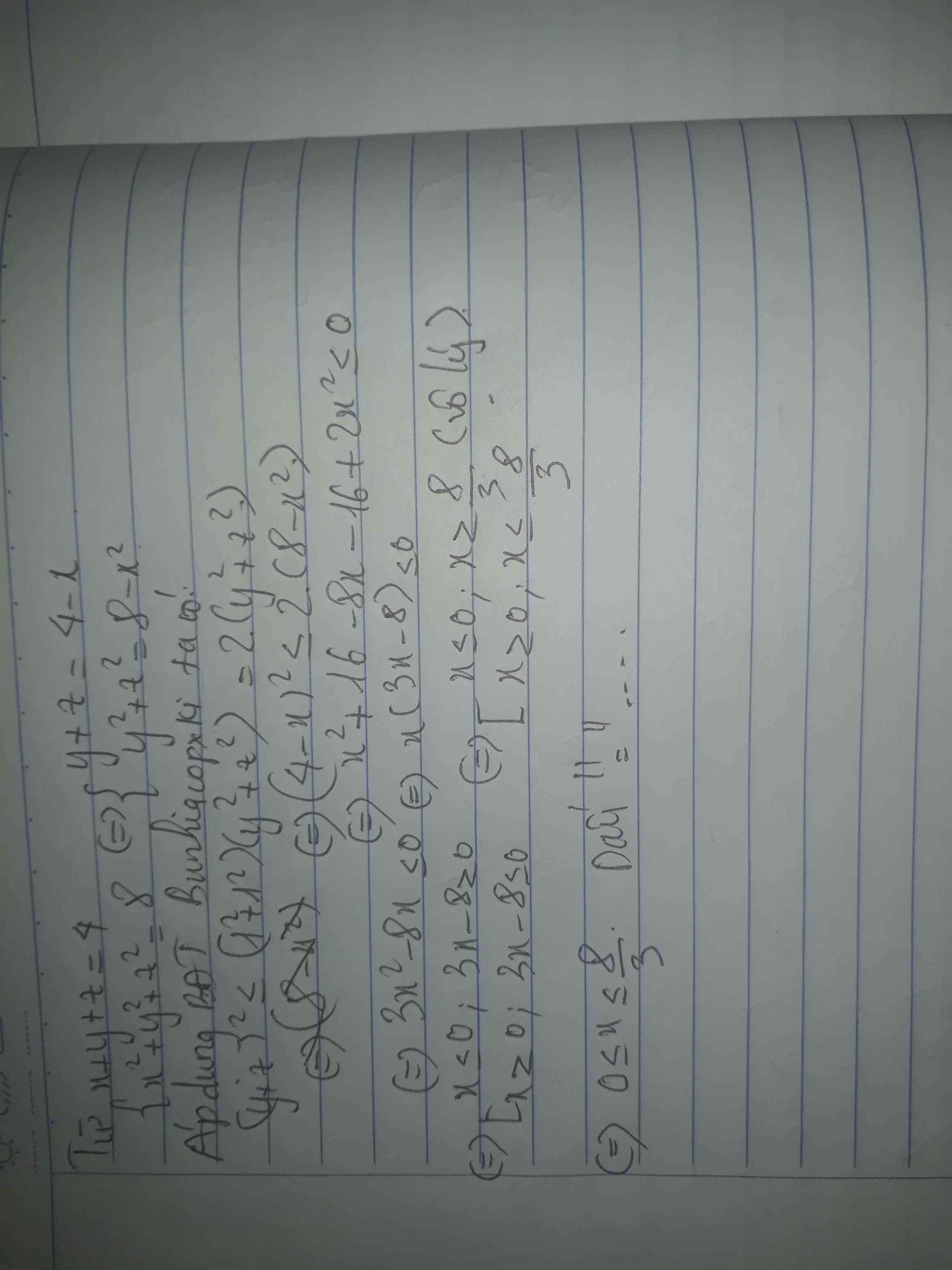
Đúng 3
Bình luận (2)
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
. Với x,y,z là các số thực dương thỏa mãn\(5\left(x+y+z\right)^2\ge14\left(x^2+y^2+z^2\right)\).Tìm GTNN và GTLN của
Q=\(\dfrac{2x+z}{2z+x}\)
Đúng 2
Bình luận (0)
1) Tìm GTNN của \(B=2\left(\frac{x^2}{y^2}+\frac{y^2}{x^2}\right)-5\left(\frac{x}{y}+\frac{y}{x}\right)\\ \left(x,y>0\right)\)
2) Tìm GTLN và GTNN của \(C=\frac{\left(x^2-y^2\right)\left(1-x^2y^2\right)}{\left(1+x^2\right)^2\left(1+y^2\right)^2}\)
Bài 1: Cho x,y thỏa mãn \(x^2+y^2-xy=4\). Tìm GTLN và GTNN của A = \(x^2+y^2\)
Bài 2: Cho x,y>0 thỏa mãn xyz=1. Tìm GTNN của
E = \(\frac{1}{x^3\left(y+z\right)}+\frac{1}{y^3\left(z+x\right)}+\frac{1}{z^3\left(x+y\right)}\)
Cho số thực dương x,y,z thỏa mãn : x+y+z = 1. Tìm GTNN của biểu thức:\(A=\frac{x^4}{\left(x^2+y^2\right)\left(x+y\right)}+\frac{y^4}{\left(y^2+z^2\right)\left(y+z\right)}+\frac{z^4}{\left(z^2+x^2\right)\left(z+x\right)}\)
cho x, y thuộc \(x^2+2y^2+2018\left(x+y\right)+2xy+4032=0\)
Hãy tìm GTNN và GTLN của P= X+Y+1
Tìm GTNN và GTLN của
A = \(\frac{7\left(x+y\right)^2-9\left(x-y\right)^2}{2016\left(x^2+y^2\right)}\)
\(A=\frac{7\left(x+y\right)^2-9\left(x-y\right)^2}{2016\left(x^2+y^2\right)}=\frac{-2\left(x^2+y^2\right)+32xy
}{2016\left(x^2+y^2\right)}=-\frac{1}{1008}+\frac{32xy}{2016\left(x^2+y^2\right)}\)
Áp dụng bđt cô si ta có:
\(xy\le\frac{x^2+y^2}{2}\)
\(\Rightarrow A\le-\frac{1}{1008}+\frac{16\left(x^2+y^2\right)}{2016\left(x^2+y^2\right)}=-\frac{1}{1008}+\frac{16}{2016}=\frac{1}{144}\)
Vậy maxA=1/144
GTNN để t nghĩ đã
Đúng 0
Bình luận (0)
Đỗ Ngọc Hải làm đúng nhưng đó đâu phải bđt cô-si đâu. Bđt cô-si là \(\frac{x+y}{2}\ge\sqrt{xy}\) hay TBC>=TBN mà
Đúng 0
Bình luận (0)
Cho x,y,z>0 và xyz=1. Tìm GTNN của Q = \(\dfrac{xy}{z^2\left(x+y\right)}+\dfrac{yz}{x^2\left(y+z\right)}+\dfrac{zx}{y^2\left(x+z\right)}\)


















