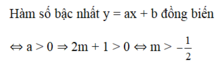Hàm số y = (2m - 5)x + 2021 đồng biến trên R khi

Những câu hỏi liên quan
Cho hàm số y (3-2m )x + 5. a)Tìm các giá trị của m để hàm số đã cho là hàm số đồng biến trên R
Đọc tiếp
Cho hàm số y = (3-2m )x + 5.
a)Tìm các giá trị của m để hàm số đã cho là hàm số đồng biến trên R
Hàm số đã cho đồng biến trên R khi và chỉ khi:
\(3-2m>0\)
\(\Leftrightarrow2m< 3\)
\(\Leftrightarrow m< \dfrac{3}{2}\)
Đúng 0
Bình luận (0)
Tìm `m` để hàm số \(y=\left(m^2-4m+4\right)x-2021\) đồng biến trên `R`.
\(m^2-4m+4=m^2-2\cdot m\cdot2+2^2=\left(m-2\right)^2>=0\forall m\)
Để hàm số \(y=\left(m^2-4m+4\right)x-2021\) đồng biến trên R thì
\(m^2-4m+4>0\)
=>\(\left(m-2\right)^2>0\)
=>m-2<>0
=>m<>2
Đúng 1
Bình luận (0)
với giá trị nào của m thì hàm số y={2m-1}x-5 đồng biến trên R
Hàm số trên có a = ( 2m - 1 )
Vậy để hàm số đồng biến thì a > 0
Hay 2m - 1 > 0 \(\Leftrightarrow\)m > \(\frac{1}{2}\)
Đúng 0
Bình luận (0)
bài 1.Cho hàm số bậc nhất y = (1-\(\sqrt{5}\))x-1
hàm số đồng biến hay nghịch biến trên R ? vì sao
tính y khi x=1+\(\sqrt{5}\)
tính x khi y=\(\sqrt{5}\)
Hàm số bậc nhất y = (1 - √5)x – 1.
a) Hàm số trên là đồng biến hay nghịch biến trên R? Vì sao?
b) Tính giá trị của y khi x = 1 + √5.
c) Tính giá trị của x khi y = √5
a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.
b) Khi x = 1 + √5 ta có:
y = (1 - √5).(1 + √5) - 1 = (1 - 5) - 1 = -5
c) Khi y = √5 ta có:
√5 = (1 - √5)x - 1
=> √5 + 1 = (1 - √5)x
![]()
(hoặc trục căn thức ở mẫu như dưới đây:
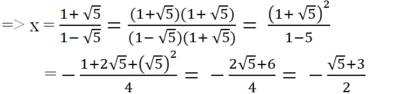
Đúng 0
Bình luận (0)
tìm các giá trị của m để hàm số sau
a) \(y=-x^3-3x^2+\left(5-m\right)x\) nghịch biến trên R
b) \(y=x^3+\left(2m-2\right)x^2+mx\) đồng biến trên R
a: \(y=-x^3-3x^2+\left(5-m\right)x\)
=>\(y'=-3x^2-3\cdot2x+5-m\)
=>\(y'=-3x^2-6x+5-m\)
Để hàm số nghịch biến trên R thì \(y'< =0\forall x\)
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(-6\right)^2-4\cdot\left(-3\right)\left(5-m\right)< =0\\-3< 0\end{matrix}\right.\)
=>\(36+12\left(5-m\right)< =0\)
=>\(36+60-12m< =0\)
=>\(-12m+96< =0\)
=>-12m<=-96
=>m>=8
b: \(y=x^3+\left(2m-2\right)\cdot x^2+mx\)
=>\(y'=3x^2+2\left(2m-2\right)\cdot x+m\)
=>\(y'=3x^2+\left(4m-4\right)x+m\)
Để hàm số đồng biến trên R thì y'>=0 với mọi x
=>\(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3>0\\\left(4m-4\right)^2-4\cdot3\cdot m< =0\end{matrix}\right.\)
=>\(16m^2-32m+16-12m< =0\)
=>\(16m^2-44m+16< =0\)
=>\(4m^2-11m+4< =0\)
=>\(\dfrac{11-\sqrt{57}}{8}< =m< =\dfrac{11+\sqrt{57}}{8}\)
Đúng 0
Bình luận (0)
Tìm m để hàm số y (2m + 1)x + m − 3 đồng biến trên R. A.
m
1
2
B.
m
1
2
C.
m
-
1
2
D.
m
-
1
2
Đọc tiếp
Tìm m để hàm số y = (2m + 1)x + m − 3 đồng biến trên R.
A. m > 1 2
B. m < 1 2
C. m < - 1 2
D. m > - 1 2
Cho hàm số y = ( \(m^2\) + 2021 ) \(x^2\). Kết luận nào sau đây đúng?
A. Hàm số nghịch biến khi x <0
B. Hàm số đồng biến khi x <0
C. Hàm số nghịch biến khi x > 0
D. Hàm số đồng biến khi x \(\le\) 0
Bài 3. Cho hàm số bậc nhất y = ax – 5 Tìm các giá trị của m để hàm số y = (2m – 4)x + 5
a) Đồng biến trên R. b. Nghịch biến trên R
a) Tìm hệ số góc a, biết đồ thị hàm số y = ax – 5 đi qua điểm A(3 ; 1)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a.
Mn giúp mình với