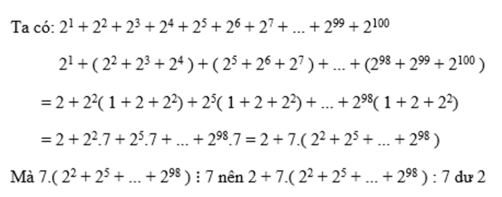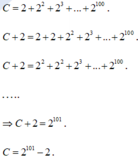H= 1+21+22+23+................+2100
Những câu hỏi liên quan
24 tháng 12 2021 lúc 15:28
Cho biểu thức A = 1 + 21 + 22 + 23 +...+ 2100 + 2101 .Chứng minh A chia hết cho 7
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2
Đúng 0
Bình luận (0)
Tính số dư khi chia:
( 2 1 + 2 2 + 2 3 + 2 4 + . . . + 2 99 + 2 100 ) cho 7
Số dư của A = 20 + 21 + 22 + 23 + .......... + 2100 khi chia cho 100 là: ................
Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Cho A = 21 + 22 + 23 + 24 + ... + 2100. Chứng minh rằng A chia hết cho 3.
Giúp mik ik ^^
*Sửa lại đề*
A = 21+ 22+ 23+ 24 + .. + 2100
A = (21+22) + (23+ 24) +...+ (299+ 2100)
A = 2.(1+2) + 23.(1+2) + .. + 299. (1+2)
A = 2.3 + 23. 3 + .. + 299.3
A = 3 . (21 + 23 + .... + 299)
Mà 3 chia hết cho 3
=> A chia hết cho 3
2+22+23+...+2100�2+22+23+...+2100
Thu gọn A và tìm n e N biết A + 2 2n
Đọc tiếp
Thu gọn A và tìm n e N biết A + 2 = 2n
29 tháng 5 2021 lúc 15:41
1+2+22+23+24+....2100 = ?
No more comment
Đặt A = \(1+2+2^2+2^3+2^4+....+2^{100}\)
2A = \(2\left(1+2+2^2+2^3+2^4+....+2^{100}\right)\)
= \(2+2^2+2^3+2^4+2^5+...+2^{101}\)
2A - A = \(\left(2+2^2+2^3+2^4+2^5+....+2^{101}\right)-\left(1+2^2+2^3+2^4+...+2^{100}\right)\)
= \(2^{101}-1\)
Đúng 2
Bình luận (0)
Nếu bạn bt lm r thì ko nên ra câu hỏi nx đâu .
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
5 tháng 8 2023 lúc 21:30
A=2100-299+298-297+...-23+22-2+1
HELP ME
\(A=2^{100}-2^{99}+2^{98}-2^{97}+....-2^3+2^2-2+1\\ A=\left(2^{100}+2^{98}+...+2\right)-\left(2^{99}+2^{97}+...+1\right)\)
Gọi \(\left(2^{100}+2^{98}+...+2\right)\)là B
\(B=\left(2^{100}+2^{98}+...+2\right)\\ 2B=2^{102}+2^{100}+.....+2^2\\ 2B-B=\left(2^{102}+2^{100}+.....+2^2\right)-\left(2^{100}+2^{98}+...+2\right)\\ B=2^{102}-2\)
Gọi \(\left(2^{99}+2^{97}+...+1\right)\) là C
\(C=\left(2^{99}+2^{97}+...+1\right)\\ 2C=2^{101}+2^{99}+....+2\\ 2C-C=\left(2^{101}+2^{99}+9^{97}+...+2\right)-\left(2^{99}+9^{97}+...+1\right)\\ C=2^{101}-1\)
\(A=B+C\\ =>A=2^{102}-2+2^{101}-1\\ A=2^{101}\left(2+1\right)-3\\ A=2^{101}\cdot3-3\\ A=3\cdot\left(2^{101}-1\right)\)
Đúng 3
Bình luận (0)
\(\dfrac{1}{2}A=2^{99}-2^{98}+...-1+\dfrac{1}{2}\\ \Rightarrow A-\dfrac{1}{2}A=2^{100}-\dfrac{1}{2}\\ \Rightarrow A=2^{101}-1\)
Đúng 0
Bình luận (0)
Có : \(S=1+2+2^2+2^3+....+2^{99}\)
\(\Rightarrow2S=2+2^2+2^3+....+2^{100}\)
\(\Rightarrow2S-S=\left(2+2^2+2^3+...+2^{100}\right)-\left(1+2+2^2+....+2^{99}\right)\)
\(\Rightarrow S=2^{100}-1< 2^{100}\)
Vậy \(S< 2^{100}\)
Đúng 1
Bình luận (0)
S=1+2+22+23+....+299
⇒2S=2+22+23+....+2100
⇒2S−S=2100-1
S=2100-1
vì 2100 -1<2100
⇒S<2100
Đúng 1
Bình luận (0)
Tính tổng: C = 2 + 2 2 + 2 3 + ... + 2 100
