Ai làm hộ Em với

Những câu hỏi liên quan
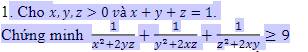 ai làm hộ em với em cần gấp;-;
ai làm hộ em với em cần gấp;-;
Vì x,y,z>0 nên áp dung bất đẳng thức Cô-si ta có:
\(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^3}{x^2+y^2+z^2+2xy+2yz+2xz}\)
mà x+y+z=1 ⇔ x2+y2+z2+2xy+2yz+2zx=1 (bình phương cả 2 vế)
nên \(\dfrac{1}{x^2+2yz}\)+\(\dfrac{1}{y^2+2xz}\)+\(\dfrac{1}{z^2+2xy}\)≥\(\dfrac{\left(1+1+1\right)^2}{\left(x+y+z\right)^2}\)=9
Đúng 1
Bình luận (0)
 ai làm hộ em với ạ !
ai làm hộ em với ạ !
 ai làm hộ em với ạ!
ai làm hộ em với ạ!
Xem thêm câu trả lời
 ai làm hộ em với ạ !
ai làm hộ em với ạ !
 ai làm hộ em với ạ !
ai làm hộ em với ạ !
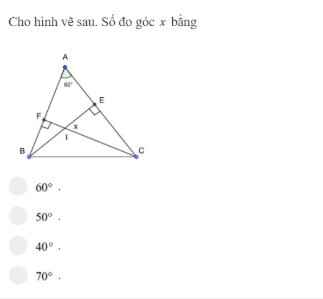
Đáp án: A - Giải thích:
Áp dụng đ/l tổng ba góc trong một tam giác vào △ABE được:
\(\hat{A}+\hat{E}+\hat{ABE}=180^o\)
\(\Rightarrow\hat{ABE}=180^o-90^o-60^o=30^o\)
Áp dụng đ/l tổng ba góc trong một tam giác vào △FBI được:
\(\hat{BFI}+\hat{FBI}+\hat{FIB}=180^o\)
\(\Rightarrow\hat{FIB}=180^o-90^o-30^o=60^o\)
- Mà \(\hat{FIB}=x\) (đối đỉnh)
\(\Rightarrow x=\hat{FBI}=60^o\)
Đúng 1
Bình luận (0)
 ai làm hộ em với ạ !
ai làm hộ em với ạ !
\(\widehat{M_2}=180^0-\widehat{M_1}=125^0\left(kề.bù\right)\)
Vì x//y nên \(\widehat{M_2}=\widehat{N_1}=125^0\)
Đúng 1
Bình luận (0)
Ai làm hộ em với ạ
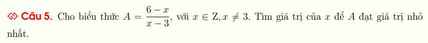
ai làm hộ em câu này với :)

ai làm hộ em VD3 này với pls :<
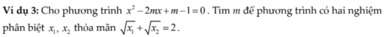
\(\Delta'=m^2-\left(m-1\right)=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy pt luôn có 2 nghiệm pb
Ta có : \(x_1+x_2+2\sqrt{x_1x_2}=4\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow\sqrt{m-1}=2-m\)
đk : m =< 2
TH1 \(m-1=2-m\Leftrightarrow m=\dfrac{3}{2}\)(tm)
TH2 \(m-1=m-2\)( vô lí )
Đúng 2
Bình luận (0)
\(\Delta'=m^2-m+1=\left(m-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0;\forall m\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m-1\end{matrix}\right.\)
Để biểu thức \(\sqrt{x_1}+\sqrt{x_2}=2\) xác định \(\Rightarrow x_1;x_2\ge0\Rightarrow\left\{{}\begin{matrix}x_1+x_2\ge0\\x_1x_2\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2m\ge0\\m-1\ge0\end{matrix}\right.\) \(\Rightarrow m\ge1\)
Khi đó:
\(\sqrt{x_1}+\sqrt{x_2}=2\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4\)
\(\Leftrightarrow2m+2\sqrt{m-1}=4\)
\(\Leftrightarrow m+\sqrt{m-1}=2\)
Đặt \(\sqrt{m-1}=t\ge0\Rightarrow m=t^2+1\)
\(\Rightarrow t^2+1+t=2\Rightarrow t^2+t-1=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-1+\sqrt{5}}{2}\\t=\dfrac{-1-\sqrt{5}}{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{m-1}=\dfrac{-1+\sqrt{5}}{2}\Rightarrow m-1=\dfrac{3-\sqrt{5}}{2}\)
\(\Rightarrow m=\dfrac{5-\sqrt{5}}{2}\)
Đúng 0
Bình luận (0)




















