a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có

\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)

Do đó: ΔMNI\(\sim\)ΔHPI(g-g)

b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)

nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)

hay \(\widehat{MNI}=\widehat{MPK}\)

Xét ΔMNI vuông tại M và ΔMPK vuông tại M có

\(\widehat{MNI}=\widehat{MPK}\)(cmt)

Do đó: ΔMNI\(\sim\)ΔMPK(g-g)

Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)

Xét ΔMNP vuông tại M và ΔMIK vuông tại M có

\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)

Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)

a: \(\widehat{C}=30^0\)

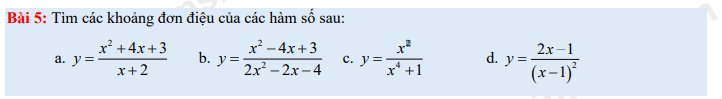
b: ĐKXĐ: \(2x^2-2x-4<>0\)

=>\(x^2-x-2<>0\)

=>(x-2)(x+1)<>0

=>x∉{2;-1}

Ta có: \(y=\frac{x^2-4x+3}{2x^2-2x-4}\)

=>\(y^{\prime}=\frac{\left(x^2-4x+3\right)^{\prime}\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(2x^2-2x-4\right)^{\prime}}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{\left(2x-4\right)\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(4x-2\right)}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{4x^3-4x^2-8x-8x^2+8x+16-\left(4x^3-2x^2-16x^2+8x+12x-6\right)}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{4x^3-12x^2+16-\left(4x^3-18x^2+20x-6\right)}{\left(2x^2-2x-4\right)^2}=\frac{6x^2-20x+22}{\left(2x^2-2x-4\right)^2}\)

Đặt y'>0

=>\(6x^2-20x+22>0\)

=>\(3x^2-10x+11>0\)

=>\(x^2-\frac{10}{3}x+\frac{11}{3}>0\)

=>\(x^2-\frac{10}{3}x+\frac{25}{9}+\frac{11}{3}-\frac{25}{9}>0\)

=>\(\left(x-\frac53\right)^2+\frac89>0\) (luôn đúng)

=>Hàm số đồng biến trên các khoảng xác định của nó

=>Hàm số đồng biến trên các khoảng (-∞;-1); (-1;2); (2;+∞)

d: \(y=\frac{2x-1}{\left(x-1\right)^2}\) (ĐKXĐ: x<>1)

=>\(y=\frac{2x-1}{x^2-2x+1}\)

=>\(y^{\prime}=\frac{\left(2x-1\right)^{\prime}\left(x^2-2x+1\right)-\left(2x-1\right)\left(x^2-2x+1\right)^{\prime}}{\left(x^2-2x+1\right)^2}\)

=>\(y^{\prime}=\frac{2\left(x^2-2x+1\right)-\left(2x-1\right)\left(2x-2\right)}{\left(x^2-2x+1\right)^2}=\frac{2x^2-4x+2-\left(4x^2-6x+2\right)}{\left(x^2-2x+1\right)^2}\)

\(=\frac{2x^2-4x+2-4x^2+6x-2}{\left(x^2-2x+1\right)^2}=\frac{-2x^2+2x}{\left(x^2-2x+1\right)^2}=\frac{-2x\left(x-1\right)}{\left(x^2-2x+1\right)^2}\)

Đặt y'<0

=>-2x(x-1)<0

=>x(x-1)>0

=>\(\left[\begin{array}{l}x>1\\ x<0\end{array}\right.\)

=>Hàm số nghịch biến trên các khoảng (1;+∞) và (-∞;0)

Đặt y'>0

=>-2x(x-1)>0

=>x(x-1)<0

=>0<x<1

=>Hàm số đồng biến trên khoảng (0;1)

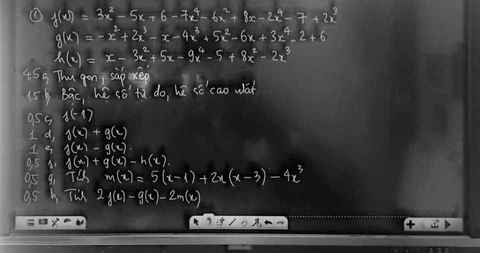
a: \(f\left(x\right)=x^4\left(-7-2\right)+2x^3+x^2\left(3-6\right)+x\left(-5+8\right)+6-7\)

\(=-9x^4+2x^3-3x^2+3x-1\)

\(g\left(x\right)=3x^4-2x^3+4x^2-7x+4\)

\(h\left(x\right)=-9x^4-2x^3+5x^2+6x-5\)

b: Bậc của f(x) là 4

Hệ số tự do của f(x) là -1

Hệ số cao nhất là -9

Bậc của g(x) là 4

Hệ số tự do là 4

Hệ số cao nhất là 3

Bậc của h(x) là 4

Hệ số tự do là -5

Hệ số cao nhất là -9

a: ΔOCB cân tại O

mà OI là đường trung tuyến

nên OI vuông góc CB

Vì góc OIA=góc OMA=góc ONA

nên O,M,N,I,A cùng thuộc 1 đường tròn

b: Xét ΔABN và ΔANC có

góc ABN=góc ANC

góc BAN chung

=>ΔABN đồng dạng với ΔANC
=>AB/AN=AN/AC

=>AN^2=AB*(AB+BC)

=>4*(BC+4)=6^2=36

=>BC=5cm

Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:

\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)

Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:

\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)

M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'

\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)

Gọi \(d_1\) là ảnh của d qua phép đối xứng trục

Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:

\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)

Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d

Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:

\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)

Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:

\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)

B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'

\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)

\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)

\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt

Phương trình \(d_1\):

\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)

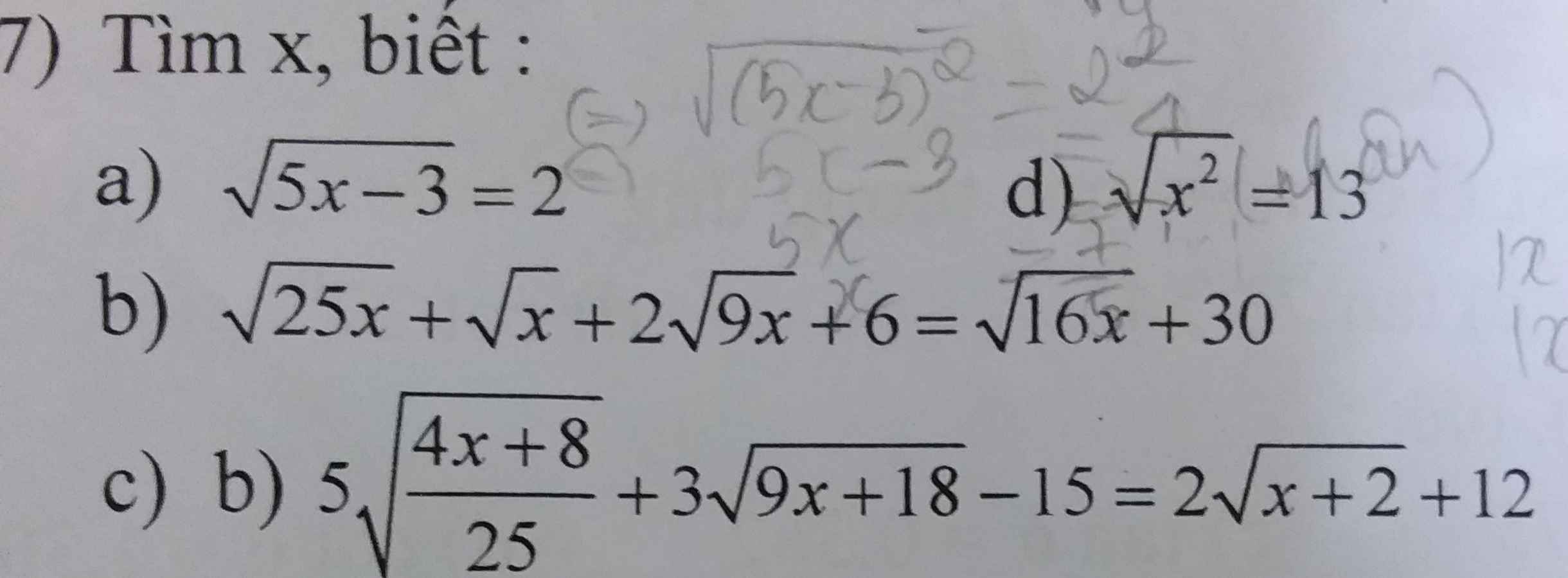
\(a,\Leftrightarrow5x-3=4\Leftrightarrow x=\dfrac{12}{5}\\ b,ĐK:x\ge0\\ PT\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}+6=4\sqrt{x}+30\\ \Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\\ c,ĐK:x\ge-2\\ PT\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-15=2\sqrt{x+2}+12\\ \Leftrightarrow9\sqrt{x+2}=27\\ \Leftrightarrow\sqrt{x+2}=3\\ \Leftrightarrow x+2=9\\ \Leftrightarrow x=7\left(tm\right)\\ d,\Leftrightarrow\left|x\right|=13\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-13\end{matrix}\right.\)

a: \(\Leftrightarrow5x-3=4\)

hay \(x=\dfrac{7}{5}\)

b) ĐKXĐ: \(x\ge0\)

\(pt\Leftrightarrow5\sqrt{x}+\sqrt{x}+6\sqrt{x}-4\sqrt{x}=30-6\)

\(\Leftrightarrow8\sqrt{x}=24\Leftrightarrow\sqrt{x}=3\Leftrightarrow x=9\left(tm\right)\)

c) ĐKXĐ: \(x\ge-2\)

\(pt\Leftrightarrow2\sqrt{x+2}+9\sqrt{x+2}-2\sqrt{x+2}=12+15\)

\(\Leftrightarrow9\sqrt{x+2}=27\Leftrightarrow\sqrt{x+2}=3\)

\(\Leftrightarrow x+2=9\Leftrightarrow x=7\left(tm\right)\)