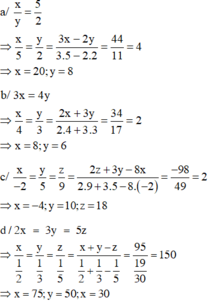a) \(\left\{{}\begin{matrix}2x+3y=5\\4x-5y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}4x+6y=10\\4x-5y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=5\\11y=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot\dfrac{9}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{27}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{28}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)

Vậy: \(x=\dfrac{14}{11};y=\dfrac{9}{11}\)

a)=(x^2-x-6)-(x^2-x-5)

=x^2-x-6-x^2+x+5

=-1

b)đề bài kì cục

\(a,\dfrac{x}{3}=\dfrac{5x}{15}\\ \dfrac{y}{5}=\dfrac{3y}{15}\\ b,\dfrac{2x}{3y}=\dfrac{2x.3xy}{y.3xy}=\dfrac{6x^2y}{3xy^2}\\ \dfrac{x+1}{xy^2}=\dfrac{3\left(x+1\right)}{3xy^2}\)

Ta có : m + n hay \(2x^2-xy-3y^2+1+x^2-2xy+3y^2-1\)

\(m+n=3x^2-3xy\)

m - n hay \(2x^2-xy-3y^2+1-x^2+2xy-3y^2+1\)

\(m-n=x^2+xy-6y^2+2\)

a.

\(\left\{{}\begin{matrix}\left(x-1\right)^2-\left(y+1\right)^2=0\\x+3y-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1-y-1\right)\left(x-1+y+1\right)=0\\x+3y-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y-2\right)\left(x+y\right)=0\\x+3y-5=0\end{matrix}\right.\)

TH1: \(\left\{{}\begin{matrix}x-y-2=0\\x+3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{4}\\y=\dfrac{3}{4}\end{matrix}\right.\)

TH2: \(\left\{{}\begin{matrix}x+y=0\\x+3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=\dfrac{5}{2}\end{matrix}\right.\)

b.

\(\left\{{}\begin{matrix}xy-2x-y+2=0\\3x+y=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\left(y-2\right)-\left(y-2\right)=0\\3x+y=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(y-2\right)=0\\3x+y=8\end{matrix}\right.\)

TH1:

\(\left\{{}\begin{matrix}x-1=0\\3x+y=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=5\end{matrix}\right.\)

TH2:

\(\left\{{}\begin{matrix}y-2=0\\3x+y=8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

c.

\(\left\{{}\begin{matrix}\left(x+y\right)^2-4\left(x+y\right)-12=0\\\left(x-y\right)^2-2\left(x-y\right)=3\end{matrix}\right.\)

Xét pt:

\(\left(x+y\right)^2-4\left(x+y\right)-12=0\)

\(\Leftrightarrow\left(x+y+2\right)\left(x+y-6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y+2=0\\x+y-6=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=-x-2\\y=6-x\end{matrix}\right.\)

TH1: \(y=-x-2\) thế vào \(\left(x-y\right)^2-2\left(x-y\right)=3\)

\(\Rightarrow\left(2x+2\right)^2-2\left(2x+2\right)=3\)

\(\Leftrightarrow4x^2+4x-3=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\Rightarrow y=-\dfrac{5}{2}\\x=-\dfrac{3}{2}\Rightarrow y=-\dfrac{1}{2}\end{matrix}\right.\)

TH2: \(y=6-x\) thế vào...

\(\left(2x-6\right)^2-2\left(2x-6\right)=3\)

\(\Leftrightarrow4x^2-28x+45=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\Rightarrow y=\dfrac{7}{2}\\y=\dfrac{9}{2}\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)

Biến đổi mỗi đa thức theo hướng làm xuất hiện thừa số x+y-2 \(M=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)

\(M=x^3+x^2y-2x^2-xy-y^2+\left(2y+y\right)+x-\left(-2+1\right)\)

\(M=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(x+y-2\right)+1\)

\(M=\left(x^2.x+x^2.y-2x^2\right)-\left(x.y+y.y-2y\right)+\left(x+y-2\right)+1\)

\(M=x^2.\left(x+y-2\right)-y.\left(x+y-2\right)+\left(x+y-2\right)+1\)

\(M=x^2.0+y.0+0+1\)

\(M=1\)

\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-2\)

\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-\left(-4+2\right)\)

\(N=\left(x^3+x^2y-2x^2\right)-\left(x^2y+xy^2-2xy\right)+\left(2x+2y-4\right)+2\)

\(N=\left(x^2x+x^2y-2x^2\right)-\left(xyx+xyy-2xy\right)+\left(2x+2y-4\right)+2\)

\(N=x^2\left(x+y-2\right)-xy\left(x+y-2\right)+2\left(x+y-2\right)+2\)

\(N=x^2.0-xy.0+2.0+2\)

\(N=2\)

\(P=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)

\(P=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left(x^2+xy-2x\right)+3\)\(P=\left(x^3x+x^3y-2x^3\right)+\left(x^2y.x+x^2yy-2x^2y\right)-\left(xx+xy-2x\right)+3\)

\(P=x^3\left(x+y-2\right)+x^2y\left(x+y-2\right)-x\left(x+y-2\right)+3\)

\(P=x^3.0+x^2y.0-x.0+3\)

\(P=3\)

Tích mình nha!

Mà bài này hình như học ở lớp 7 rồi!