Ta có:  x 2 - 4 x + 6 + 3 m = 0 ⇔ 3 m = - x 2 + 4 x - 6

Số nghiệm của phương trình  x 2 - 4 x + 6 + 3 m = 0 là số giao điểm của đường thẳng  y = 3 m  và parabol  y = - x 2 + 4 x - 6

Parabol  y = - x 2 + 4 x - 6  có hoành độ đỉnh  x = 2 ∈ - 1 ; 3 , hệ số  a = - 1 < 0  nên đồng biến khi  x < 2  và nghịch biến khi  x > 2 .

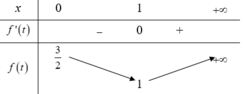
Bảng biến thiên của hàm số  y = - x 2 + 4 x - 6  trên đoạn  - 1 ; 3 :

Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn  - 1 ; 3  thì đường thẳng  y = 3 m  phải cắt parabol tại ít nhất 1 điểm có hoành độ thuộc đoạn  - 1 ; 3 .

Phương trình có nghiệm thuộc đoạn  - 1 ; 3 ⇔ - 11 ≤ 3 m ≤ - 2 ⇔ − 11 3 ≤ m ≤ − 2 3

Đáp án cần chọn là: B

Đáp án B

Phương trình viết lại  m 2 - 4 x = 3 m - 6

Phương trình đã cho vô nghiệm khi  m 2 − 4 = 0 3 m − 6 ≠ 0 ⇔ m = ± 2 m ≠ 2 ⇔ m = − 2

Do đó, phương trình đã cho có nghiệm khi m ≠ −2.

Đáp án cần chọn là: B

Vậy để bất phương trình có nghiệm thực thì  m ≥ 1

Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.

mình trình bày hơi dài mong bạn thông cảm   

Chọn B

Điều kiện: ,

đặt .

Khi đó phương trình trở thành .

Tìm GTLN – GTNN của hàm .