
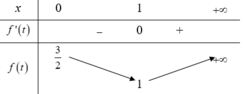
Vậy để bất phương trình có nghiệm thực thì m ≥ 1


Vậy để bất phương trình có nghiệm thực thì m ≥ 1
Cho bất phương trình 3 + x + 1 - x ≤ m + 1 - x 2 - 2 x . Tìm tất cả các giá trị thực của tham số m để bất phương trình có nghiệm thực.
A. m ≥ 25 4
B. m ≥ 4
C. m ≥ 6
D. m ≥ 7
Tìm tất cả các giá trị thực của tham số m để bất phương trình ( m + 1 ) x 2 - 2 ( m + 1 ) x + 4 ≥ 0 ( 1 ) có tập nghiệm S = ℝ ?
A. m > - 1
B. - 1 ≤ m ≤ 3
C. - 1 < m ≤ 3
D. - 1 < m < 3
Tìm tất cả các giá trị thực của tham số m để bất phương trình 4 x - m . 2 x + 1 + 3 - 2 m ≤ 0 có nghiệm thực
A. m ≥ 2
B. m ≤ 3
C. m ≤ 5
D. m ≥ 1
Tìm tất cả các giá trị thực của tham số m để bất phương trình 3 x + 3 + 5 - 3 x ≤ m có nghiệm đúng với mọi x ∈ ( - ∞ ; log 3 5 ]
A. m ≥ 2 2
B. m ≥ 4
C. m ≤ 4
D. m ≤ 2 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 3 x + m - 1 3 x + m - 1 > 0 nghiệm đúng ∀ x ∈ ℝ .
A . m ∈ R
B . m > 1
C . m ≤ 1
D . m ≥ 1
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x + 3 + 5 - 2 x ≤ m nghiệm đúng với mọi x ∈ - ∞ ; log 2 5
A. m ≥ 4
B. m < 4
C. m ≥ 2 2
D. m < 2 2
Tìm tất cả các giá trị thực của tham số m để bất phương trình log 1 2 x - 1 > log 1 2 x 3 + x - m có nghiệm
A. mÎR
B. m < 2
C. m ≤ 2
D. Không tồn tại m
Tìm tất cả các giá trị thực của tham số m để phương trình log 2 x 2 − log 2 x 2 + 3 − m = 0 có nghiệm x ∈ 1 ; 8 .
A. 2 ≤ m ≤ 6
B. 6 ≤ m ≤ 9
C. 3 ≤ m ≤ 6
D. 2 ≤ m ≤ 3
Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 x 2 + x + 2 2 x + 1 > m có nghiệm trong khoảng - ∞ ; - 1
A. m ∈ - 3 ; + ∞
B. m ∈ [ - 3 ; + ∞ )
C. m ∈ - ∞ ; - 5 2
D. m ∈ ( - ∞ ; - 5 2 ]