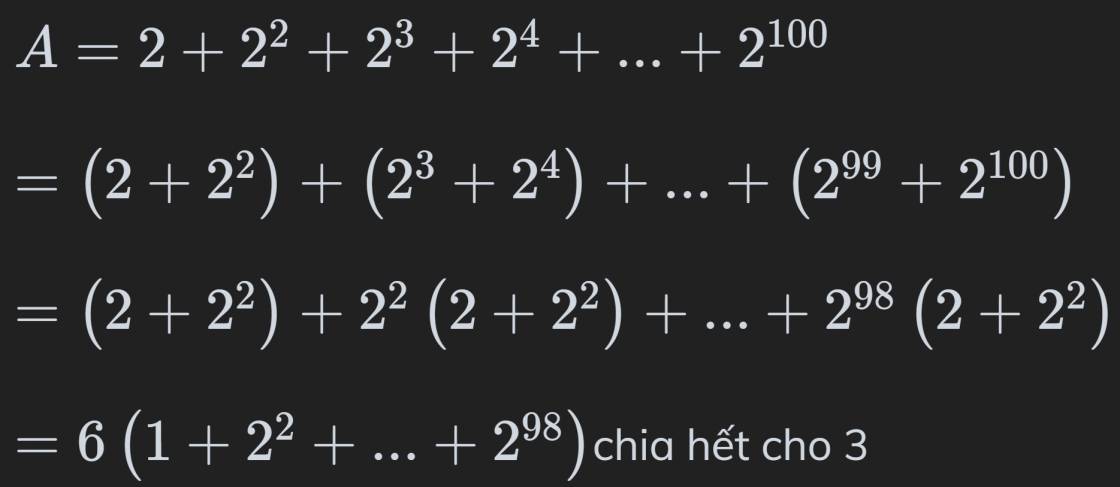Chứng minh rằng 2100 có 31 chữ số

Những câu hỏi liên quan
Chứng minh rằng : Số \(2^{100}\) viết trong hệ thập phân có 31 chữ số
Ta có \(2^{100}=\left(2^{10}\right)^{10}=1024^{10}>1000^{10}=\left(10^3\right)^{10}=10^{30}\).
Ta chứng minh \(2^{100}< 10^{31}\Leftrightarrow\dfrac{1024^{10}}{1000^{10}}< 10\).
Ta có \(\dfrac{1024^{10}}{1000^{10}}< \dfrac{1025^{10}}{1000^{10}}=\left(\dfrac{41}{40}\right)^{10}\).
Dễ thấy \(\dfrac{41}{40}< \dfrac{40}{39}< ...< \dfrac{32}{31}\Rightarrow\left(\dfrac{41}{40}\right)^{10}< \dfrac{41}{40}.\dfrac{40}{39}...\dfrac{32}{31}=\dfrac{41}{31}< 10\Rightarrow\dfrac{1024^{10}}{1000^{10}}< 10\).
Do đó \(2^{100}\) viết trong hệ thập phân có 31 chữ số.
Đúng 3
Bình luận (0)
cho biết rằng 2^10 = 1024.Chứng minh rằng 2^100 có ít nhất 31 chữ số
a. Chứng minh A=21+22+23+24+...+2100 chia hết cho 3
b. Chứng minh B=31+32+33+34+...+299chia hết cho 13
c. Chứng minh C=51+52+53+54+...+5105 chia hết cho 6 và 31
chứng minh rằng 2^100 là số có 31 chữ số khi viết kết quả của nó trong hệ thập phân.
chứng minh rằng 2^100 là số có 31 chữ số khi viết kết quả của nó trong hệ thập phân
Ta có:
2^100 = ﴾2^10﴿^10 = 1024^10
10^30 = ﴾10^3﴿^10 = 1000^10
Vì 1024^10 > 1000^10 nên 2^100 > 10^30 ﴾1﴿
Lại có:
2^100 = 2^31.2^63.2^6 = 2^31.512^7.64
và 10^31 = ﴾2.5﴿^31 = 2^31.5^31 = 2^31.5^28.5^3 = 2^31.625^7.125
Vì 2^31.512^7.64 < 2^31.625^7.125 nên 2^100 < 10^31﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ => 2^100 viết trong hệ thập phân có 31 chữ số
Vậy số 2^100 viết trong hệ thập phân có 31 chữ số ﴾đpcm﴿
NHỚ TK MK NHA,MK ĐANG ÂM ĐIỂM
Đúng 0
Bình luận (0)
bạn ơi ko hiểu đoạn 2^100=2^31.2^63.2^6 = 2^31.512^7.64
Đúng 0
Bình luận (0)
bạn ơi ko hiểu đoạn 2^100 = 2^31,2^63,2^6=2^31.512^7.64
Đúng 0
Bình luận (0)
Mn giúp mình với ạ!Mình cảm ơn!!!
Bài 1:Chứng minh rằng B = 2 + 22 + 23 + 24 + ........ + 299 + 2100 chia hết cho 31.
Mình cảm ơn mn ạ!Giúp mình với tối nay 20:00 mình phải nộp bài rồi!!!
![]()
\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
Đúng 5
Bình luận (1)
B=2+22+23+24+...+299+2100=2(1+22+23+24)+...+296(1+22+23+24)=2.31+26.31+...+296.31=31(2+26+...+296)⋮31
Đúng 1
Bình luận (0)
Cho A=1+2+2^2+2^3+...+2^99
Chứng minh rằng A+1 có 31 chữ số.
1.Số a có s 31 chữ số 1 số b có 38 chữ số 1
Chứng minh rằng a . b - 2 chia hết cho 3
2.Cho Dãy số 1, 2 , 16 , 10 , 15 ......n(n+1)/2
Chứng minh rằng tổng của 2 số hạng liên tiếp của dãy số bao h cững là số chính phương
Chứng minh rằng 2100 là số có 31 chữ soô khi viết theo kết quả của nó trong số thập phân
Ta có:
2100 = (210)10 = 102410
1030 = (103)10 = 100010
Vì 102410 > 100010 nên 2100 > 1030 (1)
Lại có:
2100 = 231.263.26 = 231.5127.64
và 1031 = (2.5)31 = 231.531 = 231.528.53 = 231.6257.125
Vì 231.5127.64 < 231.6257.125 nên 2100 < 1031 (2)
Từ (1) và (2) => 2100 viết trong hệ thập phân có 31 chữ số
Vậy số 2100 viết trong hệ thập phân có 31 chữ số (đpcm)
Đúng 0
Bình luận (0)