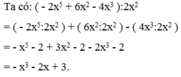(-3x5+6x2-4x3+5x4):2x2

Những câu hỏi liên quan
Thực hiện phép tính - 2 x 5 + 6 x 2 - 4 x 3 : 2 x 2
Cho các đa thức:f(x) 2x2 - x5+ 4x3 - 2x + 1g(x)4x - 3x2 + 8 - 2x5 + 7x3h(x) 1- 2x2 + 4x3 - 3x5 - 7x3Tính: a) f(x) + g(x) + h(x) b) f(x) - g(x) + h(x) c) 2f(x) + 3g(x) d) g(x) - 2h(x)giúp e với ạ giải chi tiếp giúp e
Đọc tiếp
Cho các đa thức:
f(x)= 2x2 - x5+ 4x3 - 2x + 1
g(x)=4x - 3x2 + 8 - 2x5 + 7x3
h(x)= 1- 2x2 + 4x3 - 3x5 - 7x3
Tính:
a) f(x) + g(x) + h(x) b) f(x) - g(x) + h(x)
c) 2f(x) + 3g(x) d) g(x) - 2h(x)
giúp e với ạ giải chi tiếp giúp e
Bài 4 Cho hai đa thức: P(x) 8x5 + 7x - 6x2 - 3x5 + 2x2 + 1 Q(x) 4x5 + 3x - 2x2 + x5 - 2x2 + 8 a/ Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến ? b/Tính P(x) + Q(x) c/ Tìm x để P(x) Q(x) ?
Đọc tiếp
Bài 4 Cho hai đa thức: P(x) = 8x5 + 7x - 6x2 - 3x5 + 2x2 + 1
Q(x) = 4x5 + 3x - 2x2 + x5 - 2x2 + 8
a/ Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến ?
b/Tính P(x) + Q(x) c/ Tìm x để P(x) =Q(x) ?
a, \(P\left(x\right)=5x^5-4x^2+7x+1;Q\left(x\right)=5x^5-4x^2+3x+8\)
b, \(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c, \(P\left(x\right)=Q\left(x\right)\Rightarrow7x+1=3x+8\Leftrightarrow4x=7\Leftrightarrow x=\dfrac{7}{4}\)
Đúng 0
Bình luận (0)
a/ \(P\left(x\right)=8x^5+7x-6x^2-3x^5+2x^2+1\)
\(=8x^5-3x^5-6x^2+2x^2+7x+1\)
\(=5x^5-4x^2+7x+1\)
\(Q\left(x\right)=4x^5+3x-2x^2+x^5-2x^2+8\)
\(=4x^5+x^5-2x^2-2x^2+3x+8\)
\(=5x^5-4x^2+3x+8\)
b/ \(P\left(x\right)=5x^5-4x^2+7x+1\)
+ \(Q\left(x\right)=5x^5-4x^2+3x+8\)
____________________________
\(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c/ \(P\left(x\right)=Q\left(x\right)\)
\(\Rightarrow5x^5-4x^2+7x+1=5x^5-4x^2+3x+8\)
\(\Rightarrow7x+1=3x+8\)
\(\Rightarrow4x-7=0\)
\(\Rightarrow x=\dfrac{7}{4}\)
Đúng 0
Bình luận (0)
Bài 4. Tính tổng và hiệu của các đa thức sau:
a) P(x) 5x4 + 3x2 - 3x5 + 2x - x2 - 4 +2x5 và Q(x) x5 - 4x4 + 7x - 2 + x2 - x3 + 3x4 - 2x2
b) H (x) ( 3x5 - 2x3 + 8x + 9) - ( 3x5 - x4 + 1 - x2 + 7x) và R( x) x4 + 7x3 - 4 - 4x ( x2 + 1) + 6x
ai giúp mình với
Đọc tiếp
Bài 4. Tính tổng và hiệu của các đa thức sau:
a) P(x) = 5x4 + 3x2 - 3x5 + 2x - x2 - 4 +2x5 và Q(x) = x5 - 4x4 + 7x - 2 + x2 - x3 + 3x4 - 2x2
b) H (x) = ( 3x5 - 2x3 + 8x + 9) - ( 3x5 - x4 + 1 - x2 + 7x) và R( x) = x4 + 7x3 - 4 - 4x ( x2 + 1) + 6x
ai giúp mình với
`@` `\text {Ans}`
`\downarrow`
`a)`
Thu gọn:
`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)
`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`
`= -x^5 + 5x^4 + 2x^2 + 2x - 4`
`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)
`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`
`= x^5 - x^4 - x^3 - x^2 + 7x - 2`
`@` Tổng:
`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`
`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`
`= 4x^4 - x^3 + x^2 + 9x - 6`
`@` Hiệu:
`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`
`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`
`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`
`b)`
`@` Thu gọn:
\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)
`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`
`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`
`= x^4 - 2x^3 - x^2 + 15x + 10`
\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)
`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`
`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`
`= x^4 + 3x^3 + 2x - 4`
`@` Tổng:
`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)
`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`
`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`
`= 2x^4 + x^3 - x^2 + 17x + 6`
`@` Hiệu:
`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)
`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`
`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`
`= -5x^3 - x^2 + 13x + 14`
`@` `\text {# Kaizuu lv u.}`
Đúng 3
Bình luận (0)
Cho hai đa thức: P(x) 8x5 + 7x - 6x2 - 3x5 + 2x2 + 15 Q(x) 4x5 + 3x - 2x2 + x5 - 2x2 + 8a/ Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến ?b/ Tìm nghiệm của đa thức P(x) – Q(x) ?
Đọc tiếp
Cho hai đa thức: P(x) = 8x5 + 7x - 6x2 - 3x5 + 2x2 + 15
Q(x) = 4x5 + 3x - 2x2 + x5 - 2x2 + 8
a/ Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến ?
b/ Tìm nghiệm của đa thức P(x) – Q(x) ?
a) P(x) = 5x5 - 4x2 + 7x + 15
Q(x) = 5x5 - 4x2 + 3x + 8
b) Có: P(x) - Q(x) = 4x + 7
P(x) - Q(x) = 0 <=> x = \(-\dfrac{-7}{4}\)
Đúng 1
Bình luận (0)
`a,```P(x) = 8x^5 +7x -6x^2 -3x^5 +2x^2+15`
`= (8x^5 -3x^5 ) +(-6x^2+2x^2) +7x+15`
`=5x^5 -4x^2 +7x+15`
`Q(x) =4x^5 +3x-2x^2 +x^5 -2x^2+8`
`=(4x^5+x^5) +(-2x^2 -2x^2)+3x+8`
`= 5x^5 - 4x^2 +3x+8`
`b, P(x) -Q(x)=(5x^5 -4x^2 +7x+15)-(5x^5 - 4x^2 +3x+8)`
`= 5x^5 -4x^2 +7x+15-5x^5 +4x^2 -3x-8`
`= (5x^5-5x^5)+(-4x^2+4x^2) +(7x-3x)+(15-8)`
`= 0 + 0 +4x + 7`
`=4x+7`
Đúng 3
Bình luận (1)
Câu 1:Thu gọn và tìm bậc của đa thứcA 2 + 5x2 - 3x3 + 4x2 - 2x - x2 + 6x5B 3x5y3 - 4x4y3 + 2x4y3 + 7xy2 - 3x5y3Câu 2: Thu gọn và sắp xếp theo lũy thừa giảm dầna) 8x5 - 6x2 + 7x - 3x5 + 2x2 + 15b) -9 + 5x7 - 6x2 - 11x7 + 7x2 + x5
Đọc tiếp
Câu 1:Thu gọn và tìm bậc của đa thức
A= 2 + 5x2 - 3x3 + 4x2 - 2x - x2 + 6x5
B= 3x5y3 - 4x4y3 + 2x4y3 + 7xy2 - 3x5y3
Câu 2: Thu gọn và sắp xếp theo lũy thừa giảm dần
a) 8x5 - 6x2 + 7x - 3x5 + 2x2 + 15
b) -9 + 5x7 - 6x2 - 11x7 + 7x2 + x5
Câu 1:
A=2+5x²−3x³+4x²−2x−x²+6x5A=2+5x²-3x³+4x²-2x-x²+6x5
A=6x5−3x³+(5x2+4x2−x2)−2x+2A=6x5-3x³+(5x2+4x2-x2)-2x+2
A=6x5−3x3+8x2−2x+2
Bậc của đa thức là bậc 5
...............
B=3x5y3−4x4y3+2x4y3+7xy²−3x5y3
B=(3x5y3−3x5y3)+(−4x4y3+2x4y3)+7xy
B=−2x4y3+7xy2
Bậc của đa thức là bậc 7
................
Câu 2:
a)8x5−6x2+7x−3x5+2x2+
=(8x5−3x5)+(−6x2+2x2)+7x+15
=5x5−4x2+7x+15
..................
b)=-9+5x7-6x2-11x7+7x2+x5
=(5x7-11x7)+x5+(-6x2+7x2)-9
=−6x7+x5+x2−9
Đúng 1
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử:1) 8 - 12x + 6x2 - x32) 125x3 - 75x2 +15x -13) x2 - xz - 9y2 + 3xyz4) x3 -x -5x +1255) x3 + 2x2 - 6x - 276) 12x3 + 4x2 -27x - 97) 4x4 + 4x3 - x2 - x8) x6 - x4 - 9x3 + 9x29) x4 - 4x3 + 8x2 -16x + 1610) 3a2 - 6ab + 3b2 -12c211) a2 + 2ab + b2 - ac - bc12) ac - bc - a2 + 2ab - b213) (x - y + 5)2 - 2(x - y + 5) + 114) x8 + x7 + 115) x8 + x4 +116) x5 + x + 117) x3 + x2 + 418) x4 + 2x2 - 2419) x3 - 2x - 420) x2 + 4x + 3 535 x 97 :4 thôi đùa,tiêu đề thôi câu hỏi c...
Đọc tiếp
Bài 1: Phân tích đa thức thành nhân tử:1) 8 - 12x + 6x2 - x32) 125x3 - 75x2 +15x -13) x2 - xz - 9y2 + 3xyz4) x3 -x -5x +1255) x3 + 2x2 - 6x - 276) 12x3 + 4x2 -27x - 97) 4x4 + 4x3 - x2 - x8) x6 - x4 - 9x3 + 9x29) x4 - 4x3 + 8x2 -16x + 1610) 3a2 - 6ab + 3b2 -12c211) a2 + 2ab + b2 - ac - bc12) ac - bc - a2 + 2ab - b213) (x - y + 5)2 - 2(x - y + 5) + 114) x8 + x7 + 115) x8 + x4 +116) x5 + x + 117) x3 + x2 + 418) x4 + 2x2 - 2419) x3 - 2x - 420) x2 + 4x + 3 535 x 97 :4 thôi đùa,tiêu đề thôi câu hỏi chính nè 1+1=?
M(x) 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + 2x2 – 6 N(x) - 2x2 – x4 + 4x3 – x2 -5x3 + 3x + 5 + xa) Thu gọn và sắp xếp đa thức M(x), N(x) theo lũy thừa giảm của biếnb) Xác định hệ số cao nhất, hệ số tự do, bậc của các đa thức M(x), N(x).c) Tính : M(x) + N(x)d) Tính N(x) – M(x)
Đọc tiếp
M(x) = 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + 2x2 – 6
N(x) = - 2x2 – x4 + 4x3 – x2 -5x3 + 3x + 5 + x
a) Thu gọn và sắp xếp đa thức M(x), N(x) theo lũy thừa giảm của biến
b) Xác định hệ số cao nhất, hệ số tự do, bậc của các đa thức M(x), N(x).
c) Tính : M(x) + N(x)
d) Tính N(x) – M(x)
M(x) 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + 2x2 – 6 N(x) - 2x2 – x4 + 4x3 – x2 -5x3 + 3x + 5 + xa) Thu gọn và sắp xếp đa thức M(x), N(x) theo lũy thừa giảm của biếnb) Xác định hệ số cao nhất, hệ số tự do, bậc của các đa thức M(x), N(x).c) Tính : M(x) + N(x)d) Tính N(x) – M(x)
Đọc tiếp
M(x) = 3x3 + x2 + 4x4 – x – 3x3 + 5x4 + 2x2 – 6
N(x) = - 2x2 – x4 + 4x3 – x2 -5x3 + 3x + 5 + x
a) Thu gọn và sắp xếp đa thức M(x), N(x) theo lũy thừa giảm của biến
b) Xác định hệ số cao nhất, hệ số tự do, bậc của các đa thức M(x), N(x).
c) Tính : M(x) + N(x)
d) Tính N(x) – M(x)
a) Ta có: \(M\left(x\right)=3x^3+x^2+4x^4-x-3x^3+5x^4+2x^2-6\)
\(=\left(4x^4+5x^4\right)+\left(3x^3-3x^3\right)+\left(x^2+2x^2\right)-x-6\)
\(=9x^4+3x^2-x-6\)
Ta có: \(N\left(x\right)=-2x^2-x^4+4x^3-x^2-5x^3+3x+5+x\)
\(=-x^4+\left(4x^3-5x^3\right)+\left(-2x^2-x^2\right)+\left(3x+x\right)+5\)
\(=-x^4-x^3-3x^2+4x+5\)
c) Ta có: M(x)+N(x)
\(=9x^4+3x^2-x-6-x^4-x^3-3x^2+4x+5\)
\(=8x^4-x^3+3x-1\)
Đúng 2
Bình luận (0)