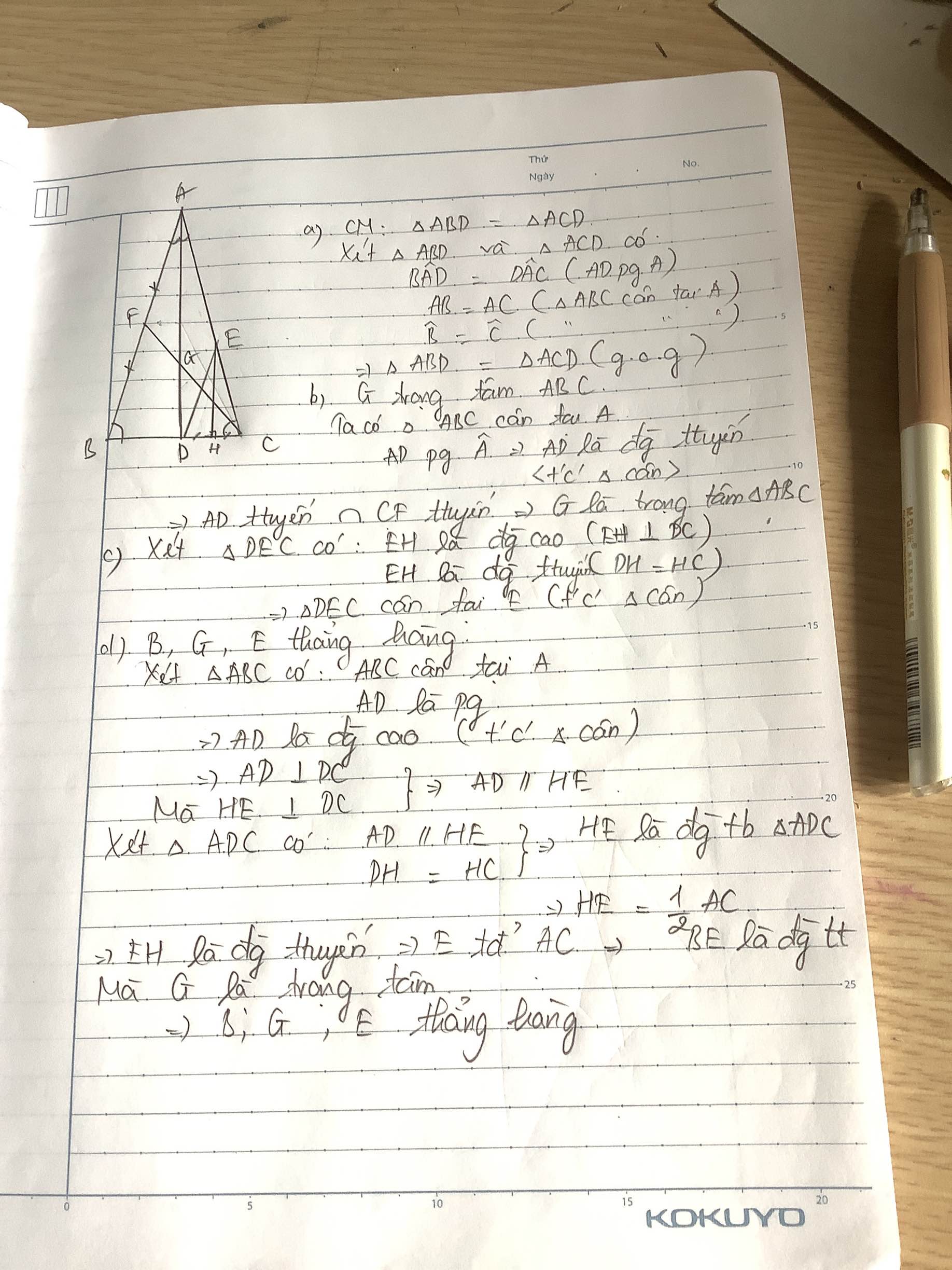Cho tam giác ABC cân tại góc A , kẻ AP là phân giác của góc BAC . Hỏi AD có là đường trung tuyến của tam giác ABC không?

Những câu hỏi liên quan
cho tam giác ABC cân tại A kẻ từ tia phân giác AD(D thuộc BC) của góc BAC;chưng minh rằng AD là đường trung tuyến của tam giác ABC
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
AB = AC (gt)
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\) (do AD là tia phân giác)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BD=CD\) (hai cạnh tương ứng)
\(\Rightarrow D\) là trung điểm của BC
\(\Rightarrow AD\) là đường trung tuyến của \(\Delta ABC\)
Đúng 3
Bình luận (0)
Ta co: ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường trung tuyến của ΔABC
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A,có góc BAC nhọn.Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a,Chứng minh:Tam giác ABD=ACD
b,Vẽ đường trung tuyến CF của Tam giác ABC cắt cạnh AD tại G.Chứng minh G là trọng tâm của tam giác ABC
a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Đúng 0
Bình luận (0)
a) Ta có: ΔABD=ΔACD(cmt)
nên BD=CD(Hai cạnh tương ứng)
mà B,D,C thẳng hàng
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(D là trung điểm của BC)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Đúng 1
Bình luận (0)
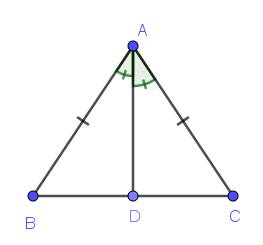
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.d) Chứng minh ba điểm B, G, E thẳng hàng và AD BD.Cả hình nữa nhé, làm nhanh giúp mình với mai nộp rồi:
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD.
Cả hình nữa nhé, làm nhanh giúp mình với mai nộp rồi:<<
a: XétΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
DO đó: ΔABD=ΔACD
b: XétΔABC có
AD là đường trung tuyến
CF là đường trung tuyến
AD cắt CF tại G
Do đó: G là trọng tâm của ΔABC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.Chứng minh ba điểm B, G, E thẳng hàng và AD BD
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
Chứng minh ba điểm B, G, E thẳng hàng và AD > BD
a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Đúng 1
Bình luận (0)
b) Ta có: ΔABD=ΔACD(cmt)
nên DB=DC(hai cạnh tương ứng)
mà B,D,C thẳng hàng(gt)
nên D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Đúng 0
Bình luận (0)
c) Xét ΔADC có
H là trung điểm của DC
HE//AD(cùng vuông góc với DC)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(gt)
mà DE là đường trung tuyến ứng với cạnh AC(cmt)
nên DE=CE
hay ΔDEC cân tại E
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.a) Chứng minh ΔABD ΔACD.b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.Chứng minh ba điểm B, G, E thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D.
a) Chứng minh ΔABD = ΔACD.
b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC.
c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân.
Chứng minh ba điểm B, G, E thẳng hàng
Mình đang cần gấp giúp mình với ạ .Cảm ơn ạ
Đúng 1
Bình luận (1)
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Ta có: ΔABD=ΔACD
nên BD=CD
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC
CF là đường trung tuyến ứng với cạnh AB
AD cắt CF tại G
DO đó: G là trọng tâm của ΔBAC
Xét ΔABC có
H là trung điểm của DC
HE//AD
Do đó: E là trung điểm của AC
Ta có: ΔADC vuông tại D
mà DE là đường trung tuyến ứng với cạnh huyền AC
nên DE=CE=AE
Xét ΔDEC có ED=EC
nên ΔDEC cân tại E
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A có AD ( D thuộc BC ) là tia phân giác của góc BAC. Chứng minh : AD là đường trung tuyến
ta có:\(AD\)là tia phân giác của góc \(\widehat{BAC}\)
Mà \(\Delta ABC\)cân tại A
\(\Rightarrow\)\(AD\)là trung tuyến của\(\widehat{BAC}\)(trong \(\Delta\)cânđường phân giác đòng thời à đường trung tuyến ứng vs cạch đáy)
có thể ghi gọn hơn chỉ giải thik cho hỉu thui
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có góc BAC nhọn.Tia phân giác của góc BAC cắt BC tại D. Đường trung tuyến BE của tam giác BAC cắt cạnh AD tại G
a)c/m tam giác BAD=tam giác CAD
b)c/m G là trọng tâm tam giác ABC và GB=GC
c)c/m AD>CD
Cho tam giác ABC cân tại A. Vẽ đường trung tuyến AM. Chứng minh:
a/tam giác ABC = tam giác ACM
b/ AM là phân giác của góc BAC
Lời giải:
a) Sửa lại thành $\triangle ABM=\triangle ACM$
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (do $ABC$ là tam giác cân tại $A$)
$\widehat{ABM}=\widehat{ACM}$ (do $ABC$ là tam giác cân tại $A$)
$AM$ chung
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
b) Từ tam giác bằng nhau trên suy ra:
$\widehat{BAM}=\widehat{CAM}$ nên $AM$ là phân giác $\widehat{BAC}$
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D. a) Chứng minh ΔABD ΔACD. b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC. c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân. d) Chứng minh ba điểm B, G, E thẳng hàng và AD BD.
Đọc tiếp
Cho tam giác ABC cân tại A, có góc BAC nhọn. Qua A vẽ tia phân giác của góc BAC cắt cạnh BC tại D. a) Chứng minh ΔABD = ΔACD. b) Vẽ đường trung tuyến CF của tam giác ABC cắt cạnh AD tại G. Chứng minh G là trọng tâm của tam giác ABC. c) Gọi H là trung điểm của cạnh DC. Qua H vẽ đường thẳng vuông góc với cạnh DC cắt cạnh AC tại E. Chứng minh ΔDEC cân. d) Chứng minh ba điểm B, G, E thẳng hàng và AD > BD.